Stochastik: Unterschied zwischen den Versionen
Aus RMG-Wiki
K (→Zu Aufgabe 1) |
K (→Zu Aufgabe 2) |
||
| Zeile 17: | Zeile 17: | ||
[[Bild:Stochastik4.png]] | [[Bild:Stochastik4.png]] | ||
| − | *Also ist der Ergebnissraum wenn man Spieler 1 als A und Spieler 2 als B | + | *Also ist der Ergebnissraum wenn man Spieler 1 als A und Spieler 2 als B nennt und einen Satzsieg als G, eine Satzniederlage als V bezeichnet. |
'''Ω''' = <math>\left [ AGG,AGVG,AGVV,AVV,AVGV,AVGG,BGG,BGVG,BGVV,BVV,BVGV,BVGG \right] </math> | '''Ω''' = <math>\left [ AGG,AGVG,AGVV,AVV,AVGV,AVGG,BGG,BGVG,BGVV,BVV,BVGV,BVGG \right] </math> | ||
Version vom 1. Oktober 2008, 12:18 Uhr
Zu Aufgabe 1
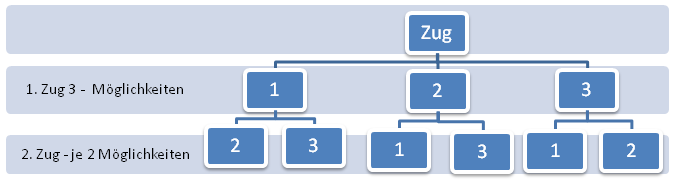
Ganz einfach, man erstellt sich ein Baumdiagramm nennt die Kugeln bspweise 1,2 und 3,
- also ist der Ergebnissraum Ω =
![\left [ 123,132,213,231,312,321 \right]](/images/math/b/7/7/b778a6de7710412422c3a2aa19a99049.png)
- (bekomme keine geschweiften Klammern hin) und damit ist die Mächtigkeit |Ω|=
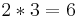
Hier nochmal das Baumdiagramm:
Zu Aufgabe 2
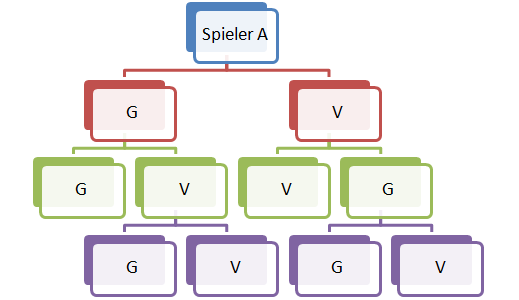
Eigentlich auch ganz einfach, man hat 2 Tennisspieler, die 2 Sätze spielen, Sieger ist derjenige, der als erster 2 Sätze gewonnen hat!
- Also ist der Ergebnissraum wenn man Spieler 1 als A und Spieler 2 als B nennt und einen Satzsieg als G, eine Satzniederlage als V bezeichnet.
Ω = ![\left [ AGG,AGVG,AGVV,AVV,AVGV,AVGG,BGG,BGVG,BGVV,BVV,BVGV,BVGG \right]](/images/math/0/6/7/0672fbc8463d06272eb089276a984131.png)
- Und damit ist die Mächtigkeit |Ω|= 6*2 = 12
Zu Aufgabe 6
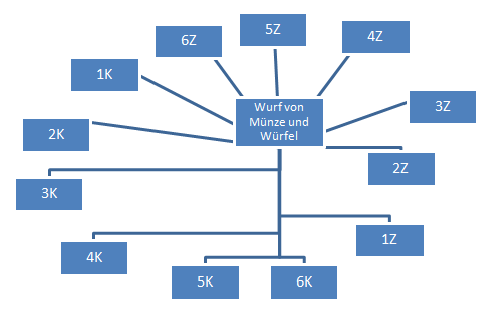
Situation: Eine Münze und ein Würfel werden geworfen und man soll den Ergebnissraum darstellen - dieser ist:
- Ω =
![\left [ 1K,2K,3K,4K,5K,6K,1Z,2Z,3Z,4Z,5Z,6Z \right]](/images/math/9/5/1/951ad46ccf5430fbe16a8ccc55485fd2.png)
- Mächtigkeit ist somit |Ω|= 6*2=12
- Man geht davon aus, dass der Würfel oder die Münze auf einer geraden Oberfläche geworfen werden und dass beide nicht auf der Kante liegen bleiben! K steht für Kopf, Z steht für Zahl!
wird bis mittwoch abend fertig sein xD