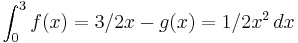Hausaufgabe - Mathe2: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Die Seite wurde neu angelegt: 1. Gegeben sind folgende Gleichungen : <math>f(x) =1/2x^2</math> <math>g(x) =3/2x</math> 2. Man geht eigentlich wie bei der ersten Aufgabe vor - Schnittpunke bestimm...) |
|||
| Zeile 1: | Zeile 1: | ||
1. Gegeben sind folgende Gleichungen : | 1. Gegeben sind folgende Gleichungen : | ||
| + | [[Bild:Aufgabe2.png|right]] | ||
| − | <math>f(x) =1/2x^2</math> | + | '''''<math>f(x) =1/2x^2</math>''''' |
| − | <math>g(x) =3/2x</math> | + | '''''<math>g(x) =3/2x</math>''''' |
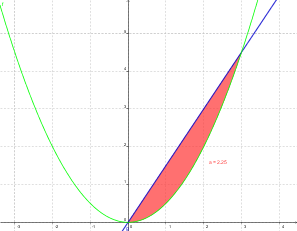
2. Man geht eigentlich wie bei der ersten Aufgabe vor - Schnittpunke bestimmen, sind in diesem Fall '''0 und 3'''! | 2. Man geht eigentlich wie bei der ersten Aufgabe vor - Schnittpunke bestimmen, sind in diesem Fall '''0 und 3'''! | ||
| − | 3. Am Ende rechnet man wieder das Integrall von f(x) minus das Integral von g(x) und sollte dann auf den Wert 9/4 kommen! | + | 3. Am Ende rechnet man wieder das Integrall von f(x) minus das Integral von g(x) und sollte dann auf den Wert '''9/4''' kommen! |
<math>\int_{0}^{3} f (x) - g(x)\,dx</math> | <math>\int_{0}^{3} f (x) - g(x)\,dx</math> | ||
| + | |||
| + | Nochmal Ausführlich: | ||
| + | |||
| + | <math>\int_{0}^{3} f (x)=3/2x - g(x)=1/2x^2\,dx</math> | ||
Version vom 24. September 2008, 15:12 Uhr
1. Gegeben sind folgende Gleichungen :
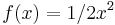
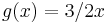
2. Man geht eigentlich wie bei der ersten Aufgabe vor - Schnittpunke bestimmen, sind in diesem Fall 0 und 3!
3. Am Ende rechnet man wieder das Integrall von f(x) minus das Integral von g(x) und sollte dann auf den Wert 9/4 kommen!
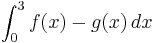
Nochmal Ausführlich: