Seite 1: Unterschied zwischen den Versionen
Aus RMG-Wiki
| (5 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
Vereinfachen Sie den Term so weit wie möglich. | Vereinfachen Sie den Term so weit wie möglich. | ||
<br/> | <br/> | ||
| − | (x+y) | + | <math>(x+y)^2-(x-y)^2 </math> |
{| | {| | ||
|width="5px"| | |width="5px"| | ||
| Zeile 11: | Zeile 11: | ||
<div style="padding:1px;background:#ddeeff;border:1px groove;"> | <div style="padding:1px;background:#ddeeff;border:1px groove;"> | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | + | <math>x^2+2xy+y - x^2 + 2xy - y2 = 4xy </math> | |
}} | }} | ||
</div> | </div> | ||
| Zeile 22: | Zeile 22: | ||
<big>'''Aufgabe 2'''</big> | <big>'''Aufgabe 2'''</big> | ||
[[Datei:BMT 10 2015 A2.jpg|220px|right]] | [[Datei:BMT 10 2015 A2.jpg|220px|right]] | ||
| − | + | Die Abbildung zeigt eine zur normalparabel kongruente Parabel mit der Gleichung y=f(x) | |
| − | + | ||
{| | {| | ||
|style="vertical-align:top"|'''a)''' | |style="vertical-align:top"|'''a)''' | ||
|width="5px"| | |width="5px"| | ||
| − | | | + | |Geben Sie einen passenden Term f(x) an. |
| − | + | ||
<div style="padding:1px;background:#ddeeff;border:1px groove;"> | <div style="padding:1px;background:#ddeeff;border:1px groove;"> | ||
| − | :{{Lösung versteckt|1= | + | :{{Lösung versteckt|1= f(x)= x<sup>2</sup>+5 |
: | : | ||
| + | |} | ||
}} | }} | ||
</div> | </div> | ||
| Zeile 40: | Zeile 39: | ||
|style="vertical-align:top"|'''b)''' | |style="vertical-align:top"|'''b)''' | ||
|width="5px"| | |width="5px"| | ||
| − | | | + | |Zeichen Sie die Gerade <math>g </math> mit der Gleichung <math>y=2-\frac{3}{2} </math> in die Abbildung ein. |
|} | |} | ||
<div style="padding:1px;background:#ddeeff;border:1px groove;"> | <div style="padding:1px;background:#ddeeff;border:1px groove;"> | ||
| − | :{{Lösung versteckt|1= | + | :{{Lösung versteckt|1= (Bild einfügen) |
: | : | ||
}} | }} | ||
| Zeile 52: | Zeile 51: | ||
|style="vertical-align:top"|'''c)''' | |style="vertical-align:top"|'''c)''' | ||
|width="5px"| | |width="5px"| | ||
| − | | | + | |Beschreiben Sie, wie man rechnerisch due Koordinaten der Punkte ermitteln kann, in denen sich die Parabel und die Gerade schneiden. |
|} | |} | ||
<div style="padding:1px;background:#ddeeff;border:1px groove;"> | <div style="padding:1px;background:#ddeeff;border:1px groove;"> | ||
| − | :{{Lösung versteckt|1= | + | :{{Lösung versteckt|1= Gleichsetzen und Auflösen <br/> |
| − | + | Alles auf eine Seite <br/> | |
| + | Lösungsformel | ||
| + | |||
| + | |||
}} | }} | ||
| + | |||
</div> | </div> | ||
| + | |||
| + | |||
| + | |} | ||
| + | |||
| + | |||
| + | |||
</div> | </div> | ||
| Zeile 67: | Zeile 76: | ||
<big>'''Aufgabe 3'''</big> | <big>'''Aufgabe 3'''</big> | ||
[[Datei:BMT 10 2015 A3.jpg|220px|right]] | [[Datei:BMT 10 2015 A3.jpg|220px|right]] | ||
| − | + | Ein mit den Ziffern von 1 bis 6 beschrifteter Laplace-Würfel wird dreimal ncheinander geworfen. | |
| − | + | Geben Sie dazu in Worten ein Ergebnis an, das die Wahrscheinlichkeit <math>(\frac {5}{6} ) ^3 </math> hat. | |
| − | :{{Lösung versteckt|1= | + | <div style="padding:1px;background:#ddeeff;border:1px groove;"> |
| + | :{{Lösung versteckt|1= Bei "Mensch ärgere dich nicht" dreimal würfeln um eine 6 zu bekommen | ||
| + | Würfelspiel, bei dem in 3 Vesuchen eine bestimmte Zahl gefragt ist | ||
: | : | ||
}} | }} | ||
</div> | </div> | ||
Aktuelle Version vom 11. Juli 2018, 08:20 Uhr
Aufgabe 1
Vereinfachen Sie den Term so weit wie möglich.
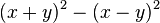
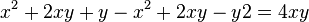
Aufgabe 2
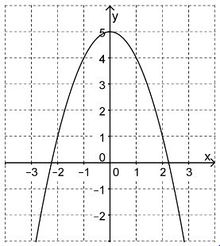
Die Abbildung zeigt eine zur normalparabel kongruente Parabel mit der Gleichung y=f(x)
| a) | Geben Sie einen passenden Term f(x) an.
}
(Bild einfügen)
Gleichsetzen und Auflösen
|
Aufgabe 3
Ein mit den Ziffern von 1 bis 6 beschrifteter Laplace-Würfel wird dreimal ncheinander geworfen.
Geben Sie dazu in Worten ein Ergebnis an, das die Wahrscheinlichkeit 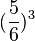 hat.
hat.
Bei "Mensch ärgere dich nicht" dreimal würfeln um eine 6 zu bekommen Würfelspiel, bei dem in 3 Vesuchen eine bestimmte Zahl gefragt ist
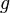 mit der Gleichung
mit der Gleichung 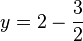 in die Abbildung ein.
in die Abbildung ein.

