Abi 2012 Analysis II Teil B: Unterschied zwischen den Versionen
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 32: | Zeile 32: | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2012_AII_TeilB_1a_Lös.jpg|700px]] |
}} | }} | ||
| Zeile 41: | Zeile 41: | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2012_AII_TeilB_1b_Lös.jpg|700px]] |
}} | }} | ||
| Zeile 50: | Zeile 50: | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2012_AII_TeilB_1c_Lös.jpg|700px]] |
}} | }} | ||
| − | '''d)''' Im Intervall ]0;2[ | + | '''d)''' Im Intervall ]0;2[ gibt es eine Stelle x<sub>0</sub>, an der der Wert der Differenz d(x)=q(x)-p(x) maximal wird. Berechnen Sie x<sub>0</sub> sowie den Wert der zugehörigen Differenz. |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2012_AII_TeilB_1d_Lös.jpg|700px]] |
}} | }} | ||
| Zeile 62: | Zeile 62: | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2012_AII_TeilB_1e_Lös.jpg|700px]] |
}} | }} | ||
| Zeile 68: | Zeile 68: | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2012_AII_TeilB_1f_Lös.jpg|700px]] |
}} | }} | ||
; Aufgabe 2 | ; Aufgabe 2 | ||
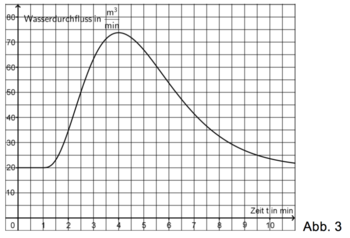
| − | Unter dem Wasserdurchfluss eines Bachs an einer bestimmten Stelle | + | Unter dem Wasserdurchfluss eines Bachs an einer bestimmten Stelle versteht man das Volumen des Wassers, das an dieser Stelle in einer bestimmten Zeit vorbeifließt. Die Funktion f beschreibt die zeitliche Entwicklung des Wasserdurchflusses eines Bachs an einer Messstelle, nachdem zum Zeitpunkt t=0 eine bachaufwärts gelegene Schleuse geöffnet wurde. Abbildung 3 zeigt den Graphen G<sub>f</sub> von f. |
[[Bild:Abi2012_AII_TeilB_2.png|center|350px]] | [[Bild:Abi2012_AII_TeilB_2.png|center|350px]] | ||
| − | '''a)''' Entnehmen Sie Abbildung 3 im Bereich t > | + | '''a)''' Entnehmen Sie Abbildung 3 im Bereich t > 1 Näherungswerte für die Koordinaten des Hochpunkts sowie für die t-Koordinaten der beiden Wendepunkte von G<sub>f</sub> und geben Sie unter Berücksichtigung dieser Näherungswerte die jeweilige Bedeutung der genannten Punkte im Sachzusammenhang an. |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2012_AII_TeilB_2a_Lös.jpg|700px]] |
}} | }} | ||
| Zeile 86: | Zeile 86: | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2012_AII_TeilB_2b_Lös.jpg|700px]] |
}} | }} | ||
| Zeile 92: | Zeile 92: | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2012_AII_TeilB_2c_Lös.jpg|700px]] |
}} | }} | ||
Aktuelle Version vom 4. April 2018, 20:55 Uhr
|
|
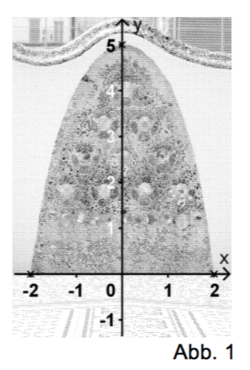
 An einer Wand im Innenhof der von Antoni Gaudi gestalteten Casa Batlló in Barcelona findet man ein Keramikkunstwerk (vgl. Abbildung 1).
Der annähernd parabelförmige obere Rand des Kunstwerks soll durch den Graphen einer ganzrationalen Funktion modellhaft dargestellt werden. Auf dem Graphen sollen bei Verwendung des ein- gezeichneten Koordinatensystems die Punkte A(-2/0), B(2/0) und C(0/5) liegen.
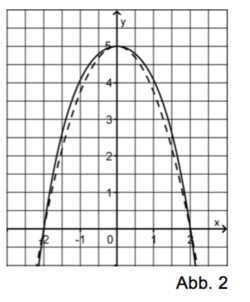
Ein den oberen Rand des Kunstwerks genauer darstellendes Modell liefert der Graph der in IR definierten ganzrationalen Funktion q vierten Grades mit q(x)=-0,11x4-0,81x2+5. Der Graph von q wird mit Gq bezeichnet. b) Weisen Sie rechnerisch nach, dass Gq symmetrisch bezüglich der y-Achse ist, durch die Punkte A und B verläuft und genau einen Extrempunkt besitzt. Abbildung 2 zeigt die Graphen von p und q.  c) Welcher der beiden dargestellten Graphen ist Gq ? Begründen Sie Ihre Antwort. d) Im Intervall ]0;2[ gibt es eine Stelle x0, an der der Wert der Differenz d(x)=q(x)-p(x) maximal wird. Berechnen Sie x0 sowie den Wert der zugehörigen Differenz. e) Berechnen Sie mithilfe der Funktion q einen Näherungswert für den Flächeninhalt A des vom Kunstwerk eingenommenen Teils der Wand. f) Die Gerade mit der Gleichung y=1,1 teilt im Modell den vom Kunstwerk eingenommenen Teil der Wand in zwei unterschiedlich gestaltete Bereiche. Beschreiben Sie, wie man mithilfe der Funktion q das Verhältnis der Flächeninhalte dieser beiden Bereiche näherungsweise bestimmen kann. Geben Sie dazu geeignete Ansätze an und kommentieren Sie diese.
Unter dem Wasserdurchfluss eines Bachs an einer bestimmten Stelle versteht man das Volumen des Wassers, das an dieser Stelle in einer bestimmten Zeit vorbeifließt. Die Funktion f beschreibt die zeitliche Entwicklung des Wasserdurchflusses eines Bachs an einer Messstelle, nachdem zum Zeitpunkt t=0 eine bachaufwärts gelegene Schleuse geöffnet wurde. Abbildung 3 zeigt den Graphen Gf von f.  a) Entnehmen Sie Abbildung 3 im Bereich t > 1 Näherungswerte für die Koordinaten des Hochpunkts sowie für die t-Koordinaten der beiden Wendepunkte von Gf und geben Sie unter Berücksichtigung dieser Näherungswerte die jeweilige Bedeutung der genannten Punkte im Sachzusammenhang an. b) Bestimmen Sie c) Bestimmen Sie mithilfe von Gf für t=4 und t=3 jeweils einen Näherungswert für die mittlere Änderungsrate von f im Zeitintervall [2;t]. Veranschaulichen Sie ihr Vorgehen in Abbildung 3 durch geeignete Steigungsdreiecke. Welche Bedeutung hat der Grenzwert der mittleren Änderungsraten für t → 2 im Sachzusammenhang
|
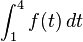näherungsweise mithilfe von Abbildung 3. Deuten Sie den Wert des Integrals im Sachzusammenhang.
