Abi 2017 Stochastik I Teil A: Unterschied zwischen den Versionen
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 29: | Zeile 29: | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2017_SI_TeilA_1ab_Lös.jpg|700px]] |
}} | }} | ||
| + | c) Die Wahrscheinlichkeit dafür, dass beim einmaligen Drehen der gelbe Sektor getroffen wird, beträgt 50%. Felix hat 100 Drehungen des Glücksrads beobachtet und festgestellt, dass bei diesen der Anteil der Drehungen, bei denen der gelbe Sektor getroffen wurde, deutlich geringer als 50% war. Er folgert: „Der Anteil der Drehungen, bei denen der gelbe Sektor getroffen wird, muss also bei den nächsten 100 Drehungen deutlich größer als 50% sein.“ Beurteilen Sie die Aussage von Felix.<br /> | ||
| + | <br /> | ||
| − | </ | + | d) Das Glücksrad wird viermal gedreht und die Abfolge der Farben als Ergebnis notiert. Bestimmen Sie die Anzahl der möglichen Ergebnisse, in denen die Farbe Blau nicht vorkommt.<br /> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2017_SI_TeilA_1cd_Lös.jpg|700px]] |
}} | }} | ||
| Zeile 58: | Zeile 50: | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
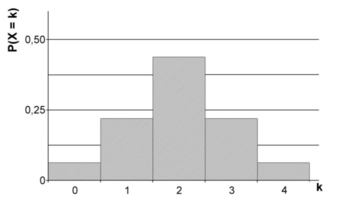
| − | ;Aufgabe | + | ;Aufgabe 2 |
| − | + | In der Abbildung ist die Wahrscheinlichkeitsverteilung einer Zufallsgröße X mit der Wertemenge {0;1;2;3;4} und dem Erwartungswert 2 dargestellt. Weisen Sie nach, dass es sich dabei nicht um eine Binomialverteilung handeln kann. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | [[Bild:ABI2017_SI_TeilA_2.png|center|350px]] | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2017_SI_TeilA_2ab_Lös.jpg|700px]] |
}} | }} | ||
Aktuelle Version vom 28. März 2018, 14:07 Uhr
|
|
Ein Glücksrad hat drei Sektoren, einen blauen, einen gelben und einen roten. Diese sind unterschiedlich groß. Die Wahrscheinlichkeit dafür, dass beim einmaligen Drehen der blaue Sektor getroffen wird, beträgt p. a)Interpretieren Sie den Term (1-p)7 im Sachzusammenhang. b) Das Glücksrad wird zehnmal gedreht. Geben Sie einen Term an, mit dem die Wahrscheinlichkeit dafür berechnet werden kann, dass der blaue Sektor genau zweimal getroffen wird  c) Die Wahrscheinlichkeit dafür, dass beim einmaligen Drehen der gelbe Sektor getroffen wird, beträgt 50%. Felix hat 100 Drehungen des Glücksrads beobachtet und festgestellt, dass bei diesen der Anteil der Drehungen, bei denen der gelbe Sektor getroffen wurde, deutlich geringer als 50% war. Er folgert: „Der Anteil der Drehungen, bei denen der gelbe Sektor getroffen wird, muss also bei den nächsten 100 Drehungen deutlich größer als 50% sein.“ Beurteilen Sie die Aussage von Felix. d) Das Glücksrad wird viermal gedreht und die Abfolge der Farben als Ergebnis notiert. Bestimmen Sie die Anzahl der möglichen Ergebnisse, in denen die Farbe Blau nicht vorkommt.  |
In der Abbildung ist die Wahrscheinlichkeitsverteilung einer Zufallsgröße X mit der Wertemenge {0;1;2;3;4} und dem Erwartungswert 2 dargestellt. Weisen Sie nach, dass es sich dabei nicht um eine Binomialverteilung handeln kann.   |
