Abi 2017 Analysis I Teil B: Unterschied zwischen den Versionen
| Zeile 10: | Zeile 10: | ||
| − | <center>[https://www.isb.bayern.de/download/ | + | <center>[https://www.isb.bayern.de/download/19428/abiturpruefung_mathematik_2017_pruefungsteil_b.pdf '''Download der Originalaufgaben'''] - [[Media:Abiturprüfung Mathematik 2017/Teil B|Lösung zum Ausdrucken]] </center> |
</td></tr></table></center> | </td></tr></table></center> | ||
| Zeile 31: | Zeile 31: | ||
[[Bild:ABI2017_AI_TeilB_1a_Lös.jpg|700px]] | [[Bild:ABI2017_AI_TeilB_1a_Lös.jpg|700px]] | ||
}} | }} | ||
| + | <br /> | ||
b) Untersuchen Sie das Monotonieverhalten von G<sub>h</sub>. Geben Sie den Grenzwert von h für x → +∞ an und begründen Sie, dass | b) Untersuchen Sie das Monotonieverhalten von G<sub>h</sub>. Geben Sie den Grenzwert von h für x → +∞ an und begründen Sie, dass | ||
| Zeile 37: | Zeile 38: | ||
[[Bild:ABI2017_AI_TeilB_1b_Lös.jpg|700px]] | [[Bild:ABI2017_AI_TeilB_1b_Lös.jpg|700px]] | ||
}} | }} | ||
| + | <br /> | ||
c) Geben Sie für die Funktion h und deren Ableitungsfunktion h'jeweils das Verhalten für x → 0 an und zeichnen Sie G<sub>h</sub> | c) Geben Sie für die Funktion h und deren Ableitungsfunktion h'jeweils das Verhalten für x → 0 an und zeichnen Sie G<sub>h</sub> | ||
| Zeile 44: | Zeile 46: | ||
[[Bild:ABI2017_AI_TeilB_1c_Lös.jpg|700px]] | [[Bild:ABI2017_AI_TeilB_1c_Lös.jpg|700px]] | ||
}} | }} | ||
| + | <br /> | ||
| + | |||
| + | Die Funtkion <math> h*:x \mapsto h(x) </math> mit Definitionsmenge [1;+∞[ unterscheidet sich von er Funktion h nur hinsichtlich der Definitionsmenge. Im Gegensatz zu h ist die Funktion h* umkehrbar. <br /> | ||
| + | |||
| + | d) Geben Sie die Definitionsmenge und die Wertemenge der Umkehrfunktion von h* an. Berechnen Sie die Koordinaten des Schnittpunkts S des Graphen von h* und der Geraden mit der Gleichung y = x . | ||
| + | : (Teilergebnis: x-Koordinate des Schnittpunkts: e<sup>4/3</sup> )<br /> | ||
| − | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2017_AI_TeilB_1d_Lös.jpg|700px]] | [[Bild:ABI2017_AI_TeilB_1d_Lös.jpg|700px]] | ||
}} | }} | ||
| + | <br /> | ||
| − | e) | + | e)Zeichnen Sie den Graphen der Umkehrfunktion von h* unter Verwendung der bisherigen Ergebnisse, insbesondere der Lage von Punkt S, in Abbildung 1 ein. |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2017_AI_TeilB_1e_Lös.jpg|700px]] | [[Bild:ABI2017_AI_TeilB_1e_Lös.jpg|700px]] | ||
}} | }} | ||
| + | <br /> | ||
| + | |||
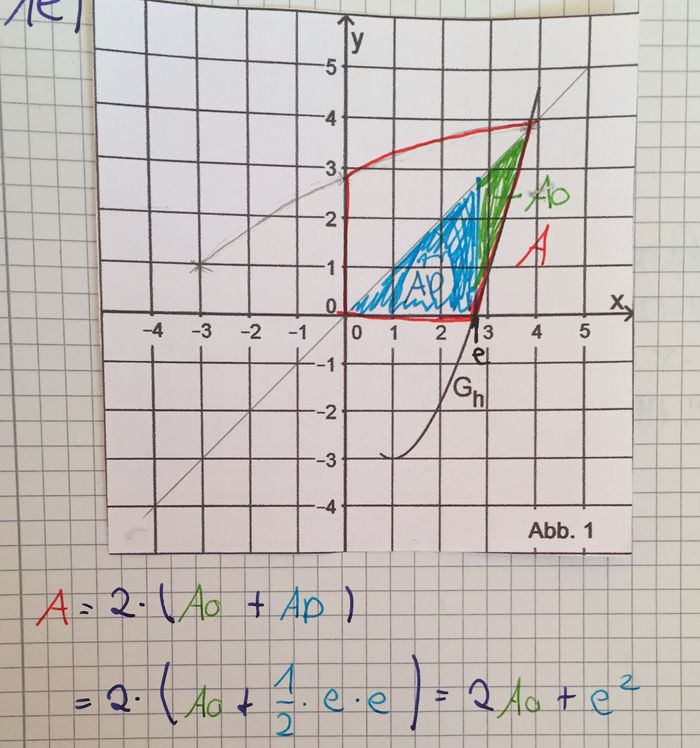
| + | f) Schraffieren Sie in Abbildung 1 ein Flächenstück, dessen Inhalt A<sub>0</sub> dem Wert des Integrals <math> \int_{e}^{x_{s}} (x-h^{*}(x))\,dx </math> entspricht, wobei x<sub>s</sub> die x-Koordinate von Punkt S ist. Der Graph von h* , der Graph der Umkehrfunktion von h* sowie die beiden Koordinatenachsen schließen im ersten Quadranten | ||
| + | ein Flächenstück mit Inhalt A ein. Geben Sie unter Verwendung von A<sub>0</sub> einen Term zur Berechnung von A an. | ||
| − | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2017_AI_TeilB_1f_Lös.jpg|700px]] | [[Bild:ABI2017_AI_TeilB_1f_Lös.jpg|700px]] | ||
| Zeile 70: | Zeile 81: | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
;Aufgabe 2 | ;Aufgabe 2 | ||
| + | Abbildung 2 zeigt den Graphen einer in [0;16] definierten Funktion <math> V:t \mapsto V(t) </math>. Sie beschreibt modellhaft das sich durch Zu- und Abfluss ändernde Volumen von Wasser in einem Becken in Abhängigkeit von der Zeit. Dabei bezeichnen t die seit Beobachtungsbeginn vergangene Zeit in Stunden und V(t) das Volumen in Kubikmetern.<br /> | ||
| − | |||
[[Bild:ABI2017_AI_TeilB_2.jpg|right|350px]] | [[Bild:ABI2017_AI_TeilB_2.jpg|right|350px]] | ||
| + | |||
| + | a) Geben Sie mithilfe von Abbildung 2 jeweils näherungsweise das Volumen des Wassers fünf Stunden nach Beobachtungsbeginn sowie den Zeitraum an, in dem das Volumen mindestens 450m<sup>3</sup> beträgt.<br /> | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2017_AI_TeilB_2a_Lös.jpg|700px]] | [[Bild:ABI2017_AI_TeilB_2a_Lös.jpg|700px]] | ||
}} | }} | ||
| + | <br /> | ||
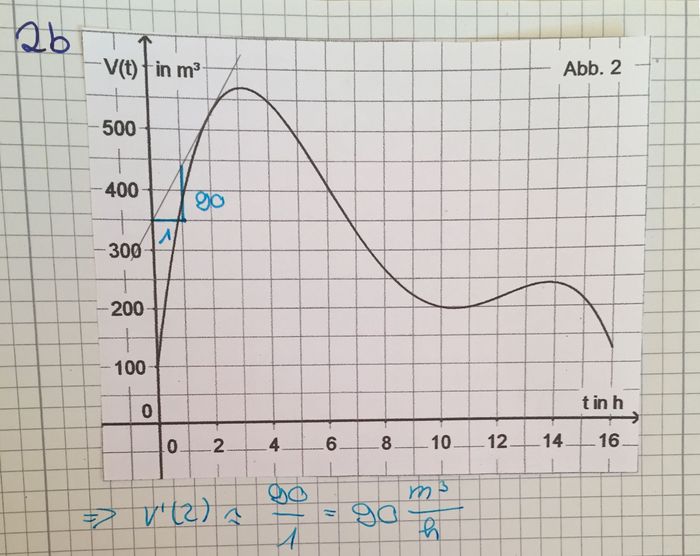
| − | b) | + | b) Bestimmen Sie anhand des Graphen der Funktion V näherungsweise die momentane Änderungsrate des Wasservolumens zwei Stunden nach Beobachtungsbeginn.<br /> |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 84: | Zeile 98: | ||
}} | }} | ||
| − | c) | + | c) Erläutern Sie, was es im Sachzusammenhang bedeutet, wenn für ein t∈[0;10]dieBeziehung V(t+6)=V(t)-350 gilt.Entscheiden Sie mithilfe von Abbildung 2, ob für t = 5 diese Beziehung gilt, und begründenSie Ihre Entscheidung.<br /> |
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2017_AI_TeilB_2c_Lös.jpg|700px]] | [[Bild:ABI2017_AI_TeilB_2c_Lös.jpg|700px]] | ||
}} | }} | ||
| + | <br /> | ||
| + | |||
| + | In einem anderen Becken ändert sich das Volumen des darin enthaltenen Wassers ebenfalls durch Zu- und Abfluss. Die momentane Änderungsrate des Volumens wird für 0 ≤ t ≤ 12 modellhaft durch die in IR definierte Funktion <math> f:t \mapsto 0,4 \cdot (2t^{3}-39t^{2}+180t </math> beschrieben. Dabei ist t die seit Beobachtungsbeginn vergangene Zeit in Stunden und g(t) die momentane Änderungsrate des Volumens in <math> \frac{m^{3}}{h}</math>. | ||
| − | d) | + | d) Begründen Sie, dass die Funktionswerte von g für 0 < t < 7,5 positiv und für 7,5 < t < 12 negativ sind. |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2017_AI_TeilB_2d_Lös.jpg|700px]] | [[Bild:ABI2017_AI_TeilB_2d_Lös.jpg|700px]] | ||
}} | }} | ||
| + | <br /> | ||
| − | e) | + | e) Erläutern Sie die Bedeutung des Werts des Integrals <math> \int_{a}^{b} g (t)\,dt </math> für 0≤a<b≤12 im Sachzusammenhang. Berechnen Sie das Volumen des |
| + | Wassers, das sich 7,5 Stunden nach Beobachtungsbeginn im Becken befindet, wenn zu Beobachtungsbeginn 150m<sup>3</sup> Wasser im Becken wa- ren. Begründen Sie, dass es sich hierbei um das maximale Wasser- volumen im Beobachtungszeitraum handelt. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
Version vom 28. März 2018, 13:01 Uhr
|
|
Gegeben ist die in IR+ definierte Funktion a) Bestimmen Sie die Gleichung der Tangente an Ghim Punkt (e | 0 )und berechnen Sie die Größe des Winkels, unter dem diese Tangente die x-Achse schneidet. (zur Kontrolle: h'(x)= 3 ⋅ lnx)
b) Untersuchen Sie das Monotonieverhalten von Gh. Geben Sie den Grenzwert von h für x → +∞ an und begründen Sie, dass [-3;+∞] die Wertemenge von h ist.
c) Geben Sie für die Funktion h und deren Ableitungsfunktion h'jeweils das Verhalten für x → 0 an und zeichnen Sie Gh im Bereich 0 ≤ x ≤ 0,75 in Abbildung 1 ein.
Die Funtkion d) Geben Sie die Definitionsmenge und die Wertemenge der Umkehrfunktion von h* an. Berechnen Sie die Koordinaten des Schnittpunkts S des Graphen von h* und der Geraden mit der Gleichung y = x .
e)Zeichnen Sie den Graphen der Umkehrfunktion von h* unter Verwendung der bisherigen Ergebnisse, insbesondere der Lage von Punkt S, in Abbildung 1 ein.
f) Schraffieren Sie in Abbildung 1 ein Flächenstück, dessen Inhalt A0 dem Wert des Integrals |
Abbildung 2 zeigt den Graphen einer in [0;16] definierten Funktion a) Geben Sie mithilfe von Abbildung 2 jeweils näherungsweise das Volumen des Wassers fünf Stunden nach Beobachtungsbeginn sowie den Zeitraum an, in dem das Volumen mindestens 450m3 beträgt.
b) Bestimmen Sie anhand des Graphen der Funktion V näherungsweise die momentane Änderungsrate des Wasservolumens zwei Stunden nach Beobachtungsbeginn. c) Erläutern Sie, was es im Sachzusammenhang bedeutet, wenn für ein t∈[0;10]dieBeziehung V(t+6)=V(t)-350 gilt.Entscheiden Sie mithilfe von Abbildung 2, ob für t = 5 diese Beziehung gilt, und begründenSie Ihre Entscheidung.
In einem anderen Becken ändert sich das Volumen des darin enthaltenen Wassers ebenfalls durch Zu- und Abfluss. Die momentane Änderungsrate des Volumens wird für 0 ≤ t ≤ 12 modellhaft durch die in IR definierte Funktion d) Begründen Sie, dass die Funktionswerte von g für 0 < t < 7,5 positiv und für 7,5 < t < 12 negativ sind.
e) Erläutern Sie die Bedeutung des Werts des Integrals |
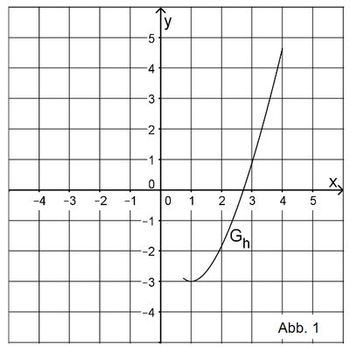
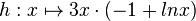 . Abbildung 1 zeigt den Graphen Gh von h im Bereich 0,75 ≤ x ≤ 4.
. Abbildung 1 zeigt den Graphen Gh von h im Bereich 0,75 ≤ x ≤ 4.



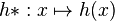 mit Definitionsmenge [1;+∞[ unterscheidet sich von er Funktion h nur hinsichtlich der Definitionsmenge. Im Gegensatz zu h ist die Funktion h* umkehrbar.
mit Definitionsmenge [1;+∞[ unterscheidet sich von er Funktion h nur hinsichtlich der Definitionsmenge. Im Gegensatz zu h ist die Funktion h* umkehrbar. 
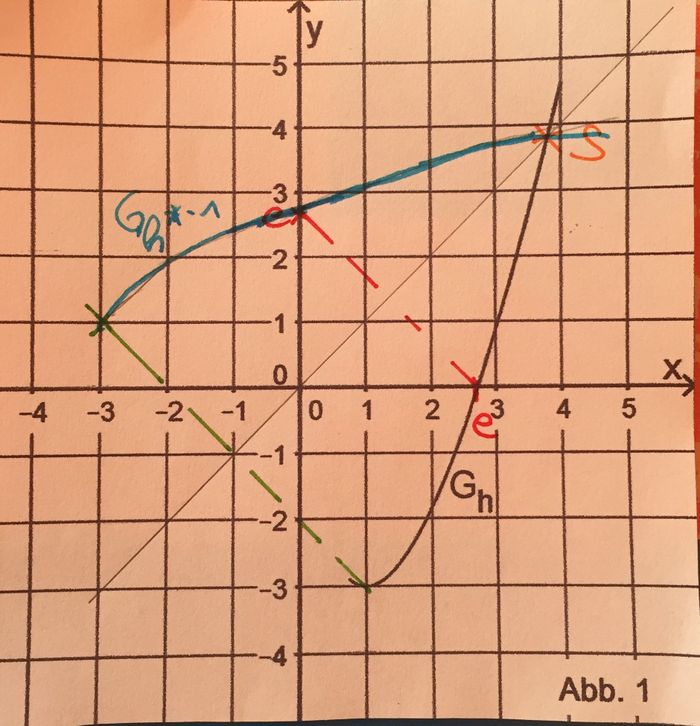
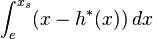 entspricht, wobei xs die x-Koordinate von Punkt S ist. Der Graph von h* , der Graph der Umkehrfunktion von h* sowie die beiden Koordinatenachsen schließen im ersten Quadranten
ein Flächenstück mit Inhalt A ein. Geben Sie unter Verwendung von A0 einen Term zur Berechnung von A an.
entspricht, wobei xs die x-Koordinate von Punkt S ist. Der Graph von h* , der Graph der Umkehrfunktion von h* sowie die beiden Koordinatenachsen schließen im ersten Quadranten
ein Flächenstück mit Inhalt A ein. Geben Sie unter Verwendung von A0 einen Term zur Berechnung von A an.
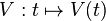 . Sie beschreibt modellhaft das sich durch Zu- und Abfluss ändernde Volumen von Wasser in einem Becken in Abhängigkeit von der Zeit. Dabei bezeichnen t die seit Beobachtungsbeginn vergangene Zeit in Stunden und V(t) das Volumen in Kubikmetern.
. Sie beschreibt modellhaft das sich durch Zu- und Abfluss ändernde Volumen von Wasser in einem Becken in Abhängigkeit von der Zeit. Dabei bezeichnen t die seit Beobachtungsbeginn vergangene Zeit in Stunden und V(t) das Volumen in Kubikmetern.

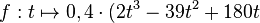 beschrieben. Dabei ist t die seit Beobachtungsbeginn vergangene Zeit in Stunden und g(t) die momentane Änderungsrate des Volumens in
beschrieben. Dabei ist t die seit Beobachtungsbeginn vergangene Zeit in Stunden und g(t) die momentane Änderungsrate des Volumens in 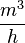 .
.

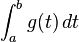 für 0≤a<b≤12 im Sachzusammenhang. Berechnen Sie das Volumen des
Wassers, das sich 7,5 Stunden nach Beobachtungsbeginn im Becken befindet, wenn zu Beobachtungsbeginn 150m3 Wasser im Becken wa- ren. Begründen Sie, dass es sich hierbei um das maximale Wasser- volumen im Beobachtungszeitraum handelt.
für 0≤a<b≤12 im Sachzusammenhang. Berechnen Sie das Volumen des
Wassers, das sich 7,5 Stunden nach Beobachtungsbeginn im Becken befindet, wenn zu Beobachtungsbeginn 150m3 Wasser im Becken wa- ren. Begründen Sie, dass es sich hierbei um das maximale Wasser- volumen im Beobachtungszeitraum handelt.


