Abi 2016 Analysis II Teil B: Unterschied zwischen den Versionen
| Zeile 7: | Zeile 7: | ||
<center><big>'''Mathematik (Bayern): Abiturprüfung 2016'''</big></center> | <center><big>'''Mathematik (Bayern): Abiturprüfung 2016'''</big></center> | ||
| − | <center><big>'''Analysis | + | <center><big>'''Analysis II - Teil B'''</big></center> |
| Zeile 23: | Zeile 23: | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
[[Bild:ABI2016_AII_TeilB_1.jpg|center|350px]] | [[Bild:ABI2016_AII_TeilB_1.jpg|center|350px]] | ||
| + | Im Rahmen eines W-Seminars modellieren Schülerinnen und Schüler einen | ||
| + | Tunnelquerschnitt, der senkrecht zum T | ||
| + | unnelverlauf liegt. Dazu beschreiben | ||
| + | sie den Querschnitt der Tunnelwand durch den Graphen einer Funktion in ei- | ||
| + | nem Koordinatensystem. Der Querschnitt | ||
| + | des Tunnelbodens liegt dabei auf der | ||
| + | x-Achse, sein Mittelpunkt M im Ur | ||
| + | sprung des Koordinatensystems; eine Längen- | ||
| + | einheit im Koordinatensystem entspricht einem Meter in der Realität. Für den | ||
| + | Tunnelquerschnitt sollen fo | ||
| + | lgende Bedingungen gelten: | ||
| + | |||
| + | I Breite des Tunnelbodens: b=10m | ||
| + | |||
| + | II Höhe des Tunnels an der höchsten Stelle: h=5m | ||
| + | |||
| + | III Der Tunnel ist auf einer Breite von mindestens 6m mindestens 4m hoch. | ||
| + | |||
| + | Eine erste Modellierung des Querschnitts der Tunnelwand verwendet die Funktion <math> p(x)\mapsto -0,2x^2+5 </math> mit Definitionsbereich <math> D_P </math> = [-5, 5] | ||
| + | |||
a) | a) | ||
Version vom 26. Juli 2017, 08:25 Uhr
|
|
Im Rahmen eines W-Seminars modellieren Schülerinnen und Schüler einen Tunnelquerschnitt, der senkrecht zum T unnelverlauf liegt. Dazu beschreiben sie den Querschnitt der Tunnelwand durch den Graphen einer Funktion in ei- nem Koordinatensystem. Der Querschnitt des Tunnelbodens liegt dabei auf der x-Achse, sein Mittelpunkt M im Ur sprung des Koordinatensystems; eine Längen- einheit im Koordinatensystem entspricht einem Meter in der Realität. Für den Tunnelquerschnitt sollen fo lgende Bedingungen gelten: I Breite des Tunnelbodens: b=10m II Höhe des Tunnels an der höchsten Stelle: h=5m III Der Tunnel ist auf einer Breite von mindestens 6m mindestens 4m hoch. Eine erste Modellierung des Querschnitts der Tunnelwand verwendet die Funktion
b) c)
|
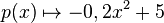 mit Definitionsbereich
mit Definitionsbereich 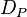 = [-5, 5]
= [-5, 5]

