Abi 2015 Analysis I Teil A: Unterschied zwischen den Versionen
| (8 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 47: | Zeile 47: | ||
;Aufgabe 2 | ;Aufgabe 2 | ||
| + | [[Bild:ABI2015_AI_TeilA_2a.jpg|right|200px]] | ||
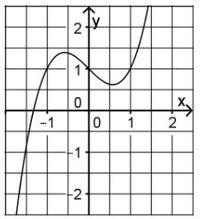
| + | Gegeben sind die in IR definierten Funktionen f, g und h mit <math>f(x) = x^2-x+1, g(x) = x^3 - x + 1, h(x) = x^4 + x^2 +1</math>. | ||
| + | a) | ||
| + | Abbildung 1 zeigt den Graphen einer der drei Funktionen. Geben Sie an, um welche Funktion es sich handelt. Begründen Sie, dass der Graph die anderen beiden Funktionen nicht darstellt. | ||
| + | |||
| + | b) | ||
| + | Die erste Ableitungsfunktion von h ist h'. Bestimmen Sie den Wert von <math> \int_{a}^{b} h'(x)\,dx</math>. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 65: | Zeile 72: | ||
;Aufgabe 3 | ;Aufgabe 3 | ||
| + | a) | ||
| + | Geben Sie einen positiven Wert für den Parameter a an, sodass die in I R definierte Funktion f : x sin ax eine Nullstelle in π6x hat. | ||
| + | b) | ||
| + | Ermitteln Sie den Wert des Parameters b, so dass die Funktion g : x x b den maximalen Definitionsbereich IR \ 2;2 besitzt. | ||
| + | |||
| + | c) | ||
| + | Erläutern Sie, dass die in IR definierte Funktion x h : x 4 e den Wertebereich;4 besitzt. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 82: | Zeile 96: | ||
;Aufgabe 4 | ;Aufgabe 4 | ||
| − | + | Abbildung 2 zeigt den Graphen einer in IR definierten differenzierbaren Funktion | |
| + | <math>f : x \mapsto g(x)</math>. Mithilfe des Newton-Verfahrens soll ein Näherungswert für die Nullstelle a von g ermittelt werden. Begründen Sie, dass | ||
| + | weder die x-Koordinate des Hochpunkts H noch die x-Koordinate des Tiefpunkts T als Startwert des Newton-Verfahrens gewählt werden kann. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 89: | Zeile 105: | ||
}} | }} | ||
| + | </td></tr></table></center> | ||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 5 | ||
| + | Gegeben ist die Funktion f mit <math>f(x) = x^3-6x^2+11x-6</math> und x∈IR. | ||
| + | |||
| + | a) Weisen Sie nach, dass der Wendepunkt des Graphen von f auf der Geradenmit der Gleichung y=x-2. | ||
| + | |||
| + | b) Der Graph von f wird verschoben. Der Punkt (2|0) des Graphen der Funktion f besitzt nach der Verschiebung die Koordinaten (3|2). Der verschobene Graph gehört zu einer Funktion h. Geben Sie eine Gleichung von h an. | ||
| + | |||
| + | :{{Lösung versteckt|1= | ||
| + | |||
| + | [[Bild:ABI2015_AI_TeilA_5ab_Lös.jpg|700px]] | ||
| + | }} | ||
</td></tr></table></center> | </td></tr></table></center> | ||
</div> | </div> | ||
Aktuelle Version vom 23. Juli 2017, 20:06 Uhr
|
|
Gegeben ist die Funktion a) Geben Sie D an. b) Bestimmen Sie die Nullstellen von f.
|
Gegeben sind die in IR definierten Funktionen f, g und h mit a) Abbildung 1 zeigt den Graphen einer der drei Funktionen. Geben Sie an, um welche Funktion es sich handelt. Begründen Sie, dass der Graph die anderen beiden Funktionen nicht darstellt. b)
Die erste Ableitungsfunktion von h ist h'. Bestimmen Sie den Wert von |
a) Geben Sie einen positiven Wert für den Parameter a an, sodass die in I R definierte Funktion f : x sin ax eine Nullstelle in π6x hat. b) Ermitteln Sie den Wert des Parameters b, so dass die Funktion g : x x b den maximalen Definitionsbereich IR \ 2;2 besitzt. c) Erläutern Sie, dass die in IR definierte Funktion x h : x 4 e den Wertebereich;4 besitzt. |
Abbildung 2 zeigt den Graphen einer in IR definierten differenzierbaren Funktion
|
Gegeben ist die Funktion f mit a) Weisen Sie nach, dass der Wendepunkt des Graphen von f auf der Geradenmit der Gleichung y=x-2. b) Der Graph von f wird verschoben. Der Punkt (2|0) des Graphen der Funktion f besitzt nach der Verschiebung die Koordinaten (3|2). Der verschobene Graph gehört zu einer Funktion h. Geben Sie eine Gleichung von h an. |
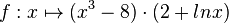 mit maximalem Definitionsbereich D.
mit maximalem Definitionsbereich D.
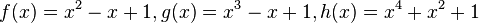 .
.
 .
.
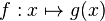 . Mithilfe des Newton-Verfahrens soll ein Näherungswert für die Nullstelle a von g ermittelt werden. Begründen Sie, dass
weder die x-Koordinate des Hochpunkts H noch die x-Koordinate des Tiefpunkts T als Startwert des Newton-Verfahrens gewählt werden kann.
. Mithilfe des Newton-Verfahrens soll ein Näherungswert für die Nullstelle a von g ermittelt werden. Begründen Sie, dass
weder die x-Koordinate des Hochpunkts H noch die x-Koordinate des Tiefpunkts T als Startwert des Newton-Verfahrens gewählt werden kann.
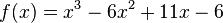 und x∈IR.
und x∈IR.

