Abi 2015 Analysis I Teil A: Unterschied zwischen den Versionen
| Zeile 101: | Zeile 101: | ||
[[Bild:ABI2015_AI_TeilA_4ab_Lös.jpg|700px]] | [[Bild:ABI2015_AI_TeilA_4ab_Lös.jpg|700px]] | ||
| + | }} | ||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 4 | ||
| + | |||
| + | |||
| + | :{{Lösung versteckt|1= | ||
| + | |||
| + | [[Bild:ABI2015_AI_TeilA_5ab_Lös.jpg|700px]] | ||
}} | }} | ||
Version vom 23. Juli 2017, 18:22 Uhr
|
|
Gegeben ist die Funktion a) Geben Sie D an. b) Bestimmen Sie die Nullstellen von f.
|
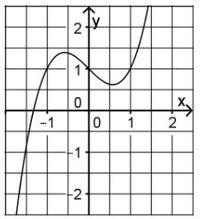
Gegeben sind die in IR definierten Funktionen f, g und h mit a) Abbildung 1 zeigt den Graphen einer der drei Funktionen. Geben Sie an, um welche Funktion es sich handelt. Begründen Sie, dass der Graph die anderen beiden Funktionen nicht darstellt. b)
Die erste Ableitungsfunktion von h ist h'. Bestimmen Sie den Wert von |
a) Geben Sie einen positiven Wert für den Parameter a an, sodass die in I R definierte Funktion f : x sin ax eine Nullstelle in π6x hat. b) Ermitteln Sie den Wert des Parameters b, so dass die Funktion g : x x b den maximalen Definitionsbereich IR \ 2;2 besitzt. c) Erläutern Sie, dass die in IR definierte Funktion x h : x 4 e den Wertebereich;4 besitzt. |
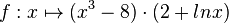 mit maximalem Definitionsbereich D.
mit maximalem Definitionsbereich D.
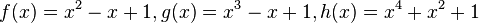 .
.
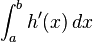 .
.

