Abi 2012 Geometrie I Teil B: Unterschied zwischen den Versionen
| Zeile 63: | Zeile 63: | ||
'''BILD FEHLT''' | '''BILD FEHLT''' | ||
Abbildung 2 zeigt ein quaderförmiges Möbelstück, das 40 cm hoch ist. Es steht mit seiner Rückseite flächenbündig an der Wand unter dem Fenster. Seine vordere Kante liegt im Modell auf der Geraden | Abbildung 2 zeigt ein quaderförmiges Möbelstück, das 40 cm hoch ist. Es steht mit seiner Rückseite flächenbündig an der Wand unter dem Fenster. Seine vordere Kante liegt im Modell auf der Geraden | ||
| − | <math> k: \vec X = \begin{pmatrix} 0 \\ 5,5 \\0,4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\0 \end{pmatrix} | + | <math> k: \vec X = \begin{pmatrix} 0 \\ 5,5 \\ 0,4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\0 \end{pmatrix} ; \lambda </math>∈ IR. |
| − | + | f) Ermitteln Sie mithilfe von Abbildung 2 die Breite b des Möbelstücks möglichst genau. | |
| − | + | Bestimmen Sie mithilfe der Gleichung der Geraden k die Tiefe t des Möbelstücks und erläutern Sie Ihr Vorgehen. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 86: | Zeile 72: | ||
}} | }} | ||
| − | + | g) Überprüfen Sie rechnerisch, ob das Fenster bei seiner Drehung am Möbelstück anstoßen kann. | |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
Version vom 20. Juli 2017, 21:05 Uhr
|
|
|
Abbildung 1 zeigt modellhaft ein Dachzimmer in der Form eines geraden Prismas. Der Boden und zwei der Seitenwände liegen in den Koordinatenebenen. Das Rechteck ABCD liegt in einer Ebene E und stellt den geneigten Teil der Deckenfläche dar. a) Bestimmen Sie eine Gleichung der Ebene E in Normalenorm.  b) Berechnen Sie den Abstand des Punkts R von der Ebene E.  Im Koordinatensystem entspricht eine Längeneinheit 1 m, d. h. das Zimmer ist an seiner höchsten Stelle 3 m hoch.
Das Rechteck GHKL mit G(2/4/2) hat die Breite c) Geben Sie die Koordinaten der Punkte L, H und K an und bestimmen Sie den Flächeninhalt des Fensters.  d) Durch das Fenster einfallendes Sonnenlicht wird im Zimmer durch parallele Geraden mit dem Richtungsvektor e) Das Fenster ist drehbar um eine Achse, die im Modell durch die Mittelpunkte der Strecken [GH] und [LK] verläuft. Die Unterkante des Fensters schwenkt dabei in das Zimmer; das Drehgelenk erlaubt eine zum Boden senkrechte Stellung der Fensterfläche. BILD FEHLT
Abbildung 2 zeigt ein quaderförmiges Möbelstück, das 40 cm hoch ist. Es steht mit seiner Rückseite flächenbündig an der Wand unter dem Fenster. Seine vordere Kante liegt im Modell auf der Geraden
f) Ermitteln Sie mithilfe von Abbildung 2 die Breite b des Möbelstücks möglichst genau. Bestimmen Sie mithilfe der Gleichung der Geraden k die Tiefe t des Möbelstücks und erläutern Sie Ihr Vorgehen. g) Überprüfen Sie rechnerisch, ob das Fenster bei seiner Drehung am Möbelstück anstoßen kann.
|
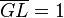. Es liegt in der Ebene E, die Punkte H und K liegen auf der Geraden CD. Das Rechteck stellt im Modell ein Dachflächenfenster dar; die Breite des Fensterrahmens soll vernachlässigt werden.
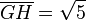
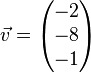repräsentiert. Eine dieser Geraden verläuft durch den Punkt G und schneidet die Seitenwand OPQR im Punkt S. Berechnen Sie die Koordinaten von S sowie die Größe des Winkels, den diese Gerade mit der Seitenwand OPQR einschließt.
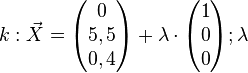∈ IR.
