Abi 2012 Analysis II Teil B: Unterschied zwischen den Versionen
| Zeile 22: | Zeile 22: | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
| − | '''BILD FEHLT''' | + | '''BILD FEHLT''' <br> |
An einer Wand im Innenhof der von Antoni Gaudi gestalteten Casa Batlló in Barcelona findet man ein Keramikkunstwerk (vgl. Abbildung 1). | An einer Wand im Innenhof der von Antoni Gaudi gestalteten Casa Batlló in Barcelona findet man ein Keramikkunstwerk (vgl. Abbildung 1). | ||
| − | Der annähernd parabelförmige obere Rand des Kunstwerks soll durch den Graphen einer ganzrationalen Funktion modellhaft dargestellt werden. Auf dem Graphen sollen bei Verwendung des ein- gezeichneten Koordinatensystems die Punkte A(-2/0), B(2/0) und C(0/5) liegen (1 LE entspricht 1m, d.h. das Kunstwerk ist 5m hoch). | + | Der annähernd parabelförmige obere Rand des Kunstwerks soll durch den Graphen einer ganzrationalen Funktion modellhaft dargestellt werden. Auf dem Graphen sollen bei Verwendung des ein- gezeichneten Koordinatensystems die Punkte A(-2/0), B(2/0) und C(0/5) liegen. <br> |
| + | (1 LE entspricht 1m, d.h. das Kunstwerk ist 5m hoch). | ||
| + | |||
| + | '''a)''' Ermitteln Sie den Term einer in IR definierten quadratischen Funktion p, deren Graph durch die Punkte A, B und C verläuft. | ||
| + | (zur Kontrolle: p(x) = -1,25x<sup>2</sup>+5) | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 31: | Zeile 35: | ||
}} | }} | ||
| − | b) | + | Ein den oberen Rand des Kunstwerks genauer darstellendes Modell liefert der Graph der in IR definierten ganzrationalen Funktion q vierten Grades mit |
| + | q(x)=-0,11x<sup>4</sup>-0,81x<sup>2</sup>+5. Der Graph von q wird mit G<sub>q</sub> bezeichnet. | ||
| + | |||
| + | '''b)''' Weisen Sie rechnerisch nach, dass G<sub>q</sub> symmetrisch bezüglich der y-Achse ist, durch die Punkte A und B verläuft und genau einen Extrempunkt besitzt. | ||
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2017_AI_TeilB_1b_Lös.jpg|700px]] | [[Bild:ABI2017_AI_TeilB_1b_Lös.jpg|700px]] | ||
}} | }} | ||
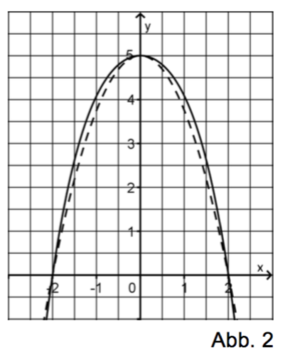
| − | c) | + | Abbildung 2 zeigt die Graphen von p und q. |
| + | [[Datei:Abitur 2012 Aufgabengruppe 2 Teil 2.png|thumb|300px]] | ||
| + | |||
| + | c) Welcher der beiden dargestellten Graphen ist G<sub>q</sub> ? Begründen Sie Ihre Antwort. | ||
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2017_AI_TeilB_1c_Lös.jpg|700px]] | [[Bild:ABI2017_AI_TeilB_1c_Lös.jpg|700px]] | ||
}} | }} | ||
| + | d) Im Intervall ]0;2[ gibt es eine Stelle x<sub>0</sub>, an der der Wert der Differenz d(x)=q(x)-p(x) maximal wird. Berechnen Sie x<sub>0</sub> sowie den Wert der zugehörigen Differenz. | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:ABI2017_AI_TeilB_1c_Lös.jpg|700px]] | ||
| + | }} | ||
| + | |||
| + | e) Berechnen Sie mithilfe der Funktion q einen Näherungswert für den Flächeninhalt A des vom Kunstwerk eingenommenen Teils der Wand. | ||
| + | |||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:ABI2017_AI_TeilB_1c_Lös.jpg|700px]] | ||
| + | }} | ||
| + | |||
| + | f) Die Gerade mit der Gleichung y=1,1 teilt im Modell den vom Kunstwerk eingenommenen Teil der Wand in zwei unterschiedlich gestaltete Bereiche. Beschreiben Sie, wie man mithilfe der Funktion q das Verhältnis der Flächeninhalte dieser beiden Bereiche näherungsweise bestimmen kann. Geben Sie dazu geeignete Ansätze an und kommentieren Sie diese. | ||
| + | |||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:ABI2017_AI_TeilB_1c_Lös.jpg|700px]] | ||
| + | }} | ||
| + | |||
| + | ; Aufgabe 2 | ||
| + | |||
| + | Unter dem Wasserdurchfluss eines Bachs an einer bestimmten Stelle ver- steht man das Volumen des Wassers, das an dieser Stelle in einer bestimmten Zeit vorbeifließt. Die Funktion f beschreibt die zeitliche Entwicklung des Wasserdurchflusses eines Bachs an einer Messstelle, nachdem zum Zeitpunkt t=0 eine bachaufwärts gelegene Schleuse geöffnet wurde. Abbildung 3 zeigt den Graphen <sub>Gf</sub> von f. | ||
| + | |||
| + | '''BILD fehlt''' | ||
| + | a) Entnehmen Sie Abbildung 3 im Bereich t > 1 Näherungswerte für die Koordinaten des Hochpunkts sowie für die t-Koordinaten der beiden Wendepunkte von G<sub>f</sub> und geben Sie unter Berücksichtigung dieser Näherungswerte die jeweilige Bedeutung der genannten Punkte im Sachzusammenhang an. | ||
| + | |||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:ABI2017_AI_TeilB_1c_Lös.jpg|700px]] | ||
| + | }} | ||
| + | |||
| + | b) Bestimmen Sie <math> \int_{1}^{4} f (t)\,dt näherungsweise mithilfe von Abbildung 3. Deuten Sie den Wert des Integrals im Sachzusammenhang. | ||
| + | |||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:ABI2017_AI_TeilB_1c_Lös.jpg|700px]] | ||
| + | }} | ||
| + | |||
| + | c) Bestimmen Sie mithilfe von G<sub>f</sub> für t=4 und t=3 jeweils einen Näherungswert für die mittlere Änderungsrate von f im Zeitintervall [2;t]. Veranschaulichen Sie ihr Vorgehen in Abbildung 3 durch geeignete Steigungsdreiecke. Welche Bedeutung hat der Grenzwert der mittleren Änderungsraten für t → 2 im Sachzusammenhang | ||
</td></tr></table></center> | </td></tr></table></center> | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:ABI2017_AI_TeilB_1c_Lös.jpg|700px]] | ||
| + | }} | ||
</div> | </div> | ||
Version vom 20. Juli 2017, 20:10 Uhr
|
|
BILD FEHLT
Ein den oberen Rand des Kunstwerks genauer darstellendes Modell liefert der Graph der in IR definierten ganzrationalen Funktion q vierten Grades mit q(x)=-0,11x4-0,81x2+5. Der Graph von q wird mit Gq bezeichnet. b) Weisen Sie rechnerisch nach, dass Gq symmetrisch bezüglich der y-Achse ist, durch die Punkte A und B verläuft und genau einen Extrempunkt besitzt. Abbildung 2 zeigt die Graphen von p und q. c) Welcher der beiden dargestellten Graphen ist Gq ? Begründen Sie Ihre Antwort. d) Im Intervall ]0;2[ gibt es eine Stelle x0, an der der Wert der Differenz d(x)=q(x)-p(x) maximal wird. Berechnen Sie x0 sowie den Wert der zugehörigen Differenz. e) Berechnen Sie mithilfe der Funktion q einen Näherungswert für den Flächeninhalt A des vom Kunstwerk eingenommenen Teils der Wand. f) Die Gerade mit der Gleichung y=1,1 teilt im Modell den vom Kunstwerk eingenommenen Teil der Wand in zwei unterschiedlich gestaltete Bereiche. Beschreiben Sie, wie man mithilfe der Funktion q das Verhältnis der Flächeninhalte dieser beiden Bereiche näherungsweise bestimmen kann. Geben Sie dazu geeignete Ansätze an und kommentieren Sie diese.
Unter dem Wasserdurchfluss eines Bachs an einer bestimmten Stelle ver- steht man das Volumen des Wassers, das an dieser Stelle in einer bestimmten Zeit vorbeifließt. Die Funktion f beschreibt die zeitliche Entwicklung des Wasserdurchflusses eines Bachs an einer Messstelle, nachdem zum Zeitpunkt t=0 eine bachaufwärts gelegene Schleuse geöffnet wurde. Abbildung 3 zeigt den Graphen Gf von f. BILD fehlt a) Entnehmen Sie Abbildung 3 im Bereich t > 1 Näherungswerte für die Koordinaten des Hochpunkts sowie für die t-Koordinaten der beiden Wendepunkte von Gf und geben Sie unter Berücksichtigung dieser Näherungswerte die jeweilige Bedeutung der genannten Punkte im Sachzusammenhang an. b) Bestimmen Sie Fehler beim Parsen(Lexikalischer Fehler): \int_{1}^{4} f (t)\,dt näherungsweise mithilfe von Abbildung 3. Deuten Sie den Wert des Integrals im Sachzusammenhang. :{{Lösung versteckt|1= [[Bild:ABI2017_AI_TeilB_1c_Lös.jpg|700px]] }} c) Bestimmen Sie mithilfe von G<sub>f</sub> für t=4 und t=3 jeweils einen Näherungswert für die mittlere Änderungsrate von f im Zeitintervall [2;t]. Veranschaulichen Sie ihr Vorgehen in Abbildung 3 durch geeignete Steigungsdreiecke. Welche Bedeutung hat der Grenzwert der mittleren Änderungsraten für t → 2 im Sachzusammenhang </td></tr></table></center> :{{Lösung versteckt|1= [[Bild:ABI2017_AI_TeilB_1c_Lös.jpg|700px]] }} </div> |