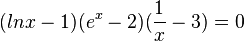Abi 2013 Analysis I Teil A: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 62: | Zeile 62: | ||
;Aufgabe 3 | ;Aufgabe 3 | ||
| − | + | Geben Sie für x ∈ IR<sup>+</sup> die Lösungen der folgenden Gleichung an: <br> | |
| + | <math> (lnx-1)(e^x-2)(\frac{1}{x} -3)=0 </math> | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
Version vom 20. Juli 2017, 12:28 Uhr
|
|
Gegeben ist die Funktion
|
Geben Sie jeweils den Term einer in IR definierten Funktion an, die die angegebene Wertemenge W hat. |
Geben Sie für x ∈ IR+ die Lösungen der folgenden Gleichung an: |
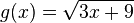 mit maximaler Definitionsmenge D.
mit maximaler Definitionsmenge D.