Benutzer:Sarah Ulrich: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 3: | Zeile 3: | ||
Die Abbildung zeigt ein rechtwinkliges Dreieck mit den Seiten r,s und t sowie den Innenwinkeln α und β. Kreuzen Sie jeweils nur die zutreffenden Aussagen an. | Die Abbildung zeigt ein rechtwinkliges Dreieck mit den Seiten r,s und t sowie den Innenwinkeln α und β. Kreuzen Sie jeweils nur die zutreffenden Aussagen an. | ||
| − | (!<math>\sin \alpha= \frac{r}{t}</math>) (<math>\cos \beta= \frac{t}{s}</math>) (<math>\tan \alpha= \frac{r}{s}</math>) (!<math>\tan \alpha= \frac{s}{s}</math>) | + | (!<math>\sin \alpha= \frac{r}{t}</math>) (<math>\cos \beta= \frac{t}{s}</math>) (<math>\tan \alpha= \frac{r}{s}</math>) (!<math>\tan \alpha= \frac{s}{s}</math>) |
(<math>r=\sqrt{s^2+t^2}</math>) (!<math>s=\sqrt{t^2-r^2}</math>) (<math>t=\sqrt{r^2-s^2}</math>) (<math>t=\sqrt{s^2-r^2}</math>) | (<math>r=\sqrt{s^2+t^2}</math>) (!<math>s=\sqrt{t^2-r^2}</math>) (<math>t=\sqrt{r^2-s^2}</math>) (<math>t=\sqrt{s^2-r^2}</math>) | ||
</div> | </div> | ||
Version vom 11. Juli 2017, 10:58 Uhr
Die Abbildung zeigt ein rechtwinkliges Dreieck mit den Seiten r,s und t sowie den Innenwinkeln α und β. Kreuzen Sie jeweils nur die zutreffenden Aussagen an.
(!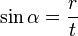 ) (
) (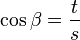 ) (
) (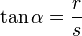 ) (!
) (!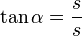 )
)
(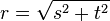 ) (!
) (!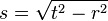 ) (
) (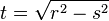 ) (
) (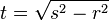 )
)

