Abi 2015 Analysis I Teil A: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 47: | Zeile 47: | ||
;Aufgabe 2 | ;Aufgabe 2 | ||
| + | Gegeben sind die in IR definierten Funktionen f, g und h mit <math>f(x) = x^2-x+1, g(x) = x^3 - x + 1, h(x) = x^4 + x^2 +1</math>. | ||
| + | a) | ||
| + | Abbildung 1 zeigt den Graphen einer der drei Funktionen. Geben Sie an, um welche Funktion es sich handelt. Begründen Sie, dass der Graph die anderen beiden Funktionen nicht darstellt. | ||
| + | |||
| + | b) | ||
| + | Die erste Ableitungsfunktion von h ist h'. Bestimmen Sie den Wert von <math> \int_{a}^{b} h'(x)\,dx</math>. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
Version vom 10. Juli 2017, 21:59 Uhr
|
|
Gegeben ist die Funktion a) Geben Sie D an. b) Bestimmen Sie die Nullstellen von f.
|
Gegeben sind die in IR definierten Funktionen f, g und h mit a) Abbildung 1 zeigt den Graphen einer der drei Funktionen. Geben Sie an, um welche Funktion es sich handelt. Begründen Sie, dass der Graph die anderen beiden Funktionen nicht darstellt. b)
Die erste Ableitungsfunktion von h ist h'. Bestimmen Sie den Wert von |
|
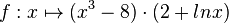 mit maximalem Definitionsbereich D.
mit maximalem Definitionsbereich D.
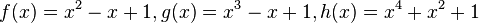 .
.
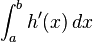 .
.

