Abi 2014 Geometrie I Teil A: Unterschied zwischen den Versionen
Aus RMG-Wiki
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 24: | Zeile 24: | ||
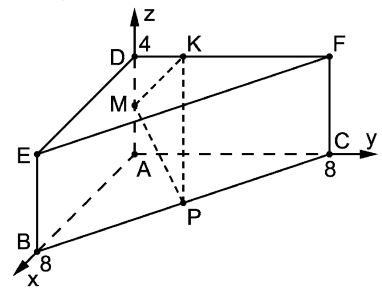
Die Abbildung zeigt ein gerades Prisma ABCDEF mit A(0|0|0), B (8|0|0), C (0|8|0) und D (0|0|4). | Die Abbildung zeigt ein gerades Prisma ABCDEF mit A(0|0|0), B (8|0|0), C (0|8|0) und D (0|0|4). | ||
| − | + | [[Datei:ABI2014 GI TeilA 1 Grafik.JPG]] | |
a) Bestimmen Sie den Abstand der Eckpunkte B und F. | a) Bestimmen Sie den Abstand der Eckpunkte B und F. | ||
| Zeile 60: | Zeile 60: | ||
</td></tr></table></center> | </td></tr></table></center> | ||
| + | |||
| + | |||
</div> | </div> | ||
Aktuelle Version vom 10. Juli 2017, 18:44 Uhr
|
|
Die Abbildung zeigt ein gerades Prisma ABCDEF mit A(0|0|0), B (8|0|0), C (0|8|0) und D (0|0|4). a) Bestimmen Sie den Abstand der Eckpunkte B und F. b) Die Punkte M und P sind die Mittelpunkte der Kanten [AD] bzw. [BC]. Der Punkt K (0|yk|4) liegt auf der Kante [DF]. Bestimmen Sie yk so, dass das Dreieck KMP in M rechtwinklig ist.
|
Gegeben ist die Ebene E : 3x2 + 4x3 = 5. a) Beschreiben Sie die besondere Lage von E im Koordinatensystem. b) Untersuchen Sie rechnerisch, ob die Kugel mit Mittelpunkt Z (1|6|3) und Radius 7 die Ebene E schneidet. |