Abi 2017 Analysis I Teil B: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 22: | Zeile 22: | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
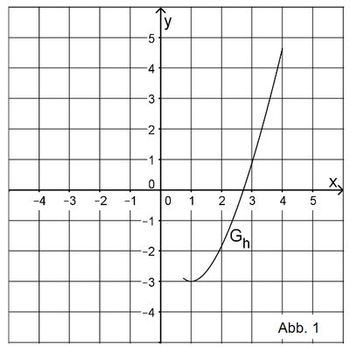
| − | Gegeben ist die in IR<sup>+</sup> definierte Funktion <math>h: x \mapsto 3x \cdot (-1 + lnx)</math>. Abbildung 1 zeigt den Graphen G<sub>h</sub> von h im Bereich 0,75 ≤ | + | Gegeben ist die in IR<sup>+</sup> definierte Funktion <math>h: x \mapsto 3x \cdot (-1 + lnx)</math>. Abbildung 1 zeigt den Graphen G<sub>h</sub> von h im Bereich 0,75 ≤ x ≤ 4. |
[[Bild:ABI2017_AI_TeilB_1a.jpg|center|350px]] | [[Bild:ABI2017_AI_TeilB_1a.jpg|center|350px]] | ||
| − | a) | + | a) Bestimmen Sie die Gleichung der Tangente an G<sub>h</sub>im Punkt (e | 0 )und berechnen Sie die Größe des Winkels, unter dem diese Tangente die x-Achse schneidet. |
| + | |||
| + | (''zur Kontrolle: h'(x)= 3 ⋅ lnx'') | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2017_AI_TeilB_1a_Lös.jpg|700px]] | [[Bild:ABI2017_AI_TeilB_1a_Lös.jpg|700px]] | ||
}} | }} | ||
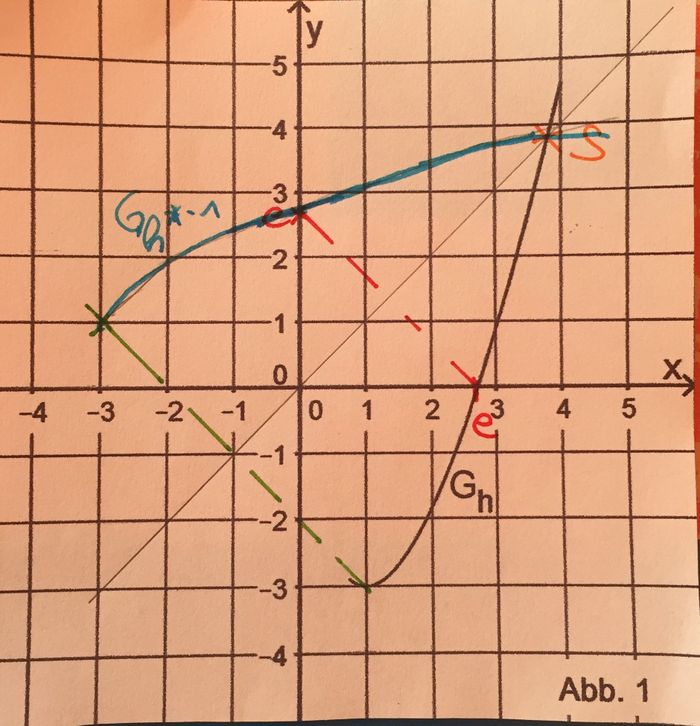
| − | b) | + | b) Untersuchen Sie das Monotonieverhalten von G<sub>h</sub>. Geben Sie den Grenzwert von h für x → +∞ an und begründen Sie, dass |
| + | [-3;+∞] die Wertemenge von h ist. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2017_AI_TeilB_1b_Lös.jpg|700px]] | [[Bild:ABI2017_AI_TeilB_1b_Lös.jpg|700px]] | ||
}} | }} | ||
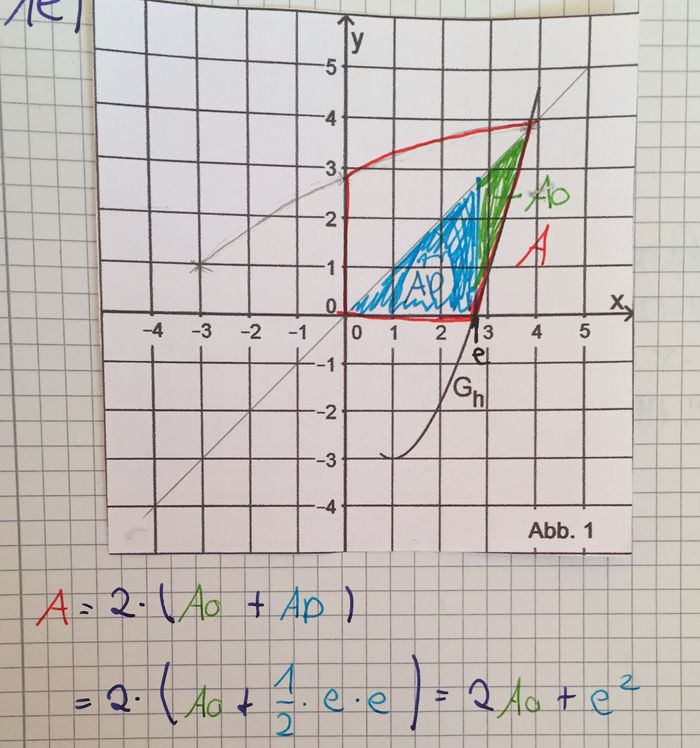
| − | c) | + | c) Geben Sie für die Funktion h und deren Ableitungsfunktion h'jeweils das Verhalten für x → 0 an und zeichnen Sie G<sub>h</sub> |
| + | im Bereich 0 ≤ x ≤ 0,75 in Abbildung 1 ein. | ||
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2017_AI_TeilB_1c_Lös.jpg|700px]] | [[Bild:ABI2017_AI_TeilB_1c_Lös.jpg|700px]] | ||
Version vom 5. Juli 2017, 22:48 Uhr
|
|
Gegeben ist die in IR+ definierte Funktion  a) Bestimmen Sie die Gleichung der Tangente an Ghim Punkt (e | 0 )und berechnen Sie die Größe des Winkels, unter dem diese Tangente die x-Achse schneidet. (zur Kontrolle: h'(x)= 3 ⋅ lnx)  b) Untersuchen Sie das Monotonieverhalten von Gh. Geben Sie den Grenzwert von h für x → +∞ an und begründen Sie, dass [-3;+∞] die Wertemenge von h ist.  c) Geben Sie für die Funktion h und deren Ableitungsfunktion h'jeweils das Verhalten für x → 0 an und zeichnen Sie Gh im Bereich 0 ≤ x ≤ 0,75 in Abbildung 1 ein.  d)  e)  f)  |
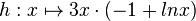. Abbildung 1 zeigt den Graphen Gh von h im Bereich 0,75 ≤ x ≤ 4.
