Abitur Mathematik: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 59: | Zeile 59: | ||
a) Ermitteln Sie die Nullstelle der Funktion f. | a) Ermitteln Sie die Nullstelle der Funktion f. | ||
| − | b) Die Tangente an den Graphen von f im Punkt | + | b) Die Tangente an den Graphen von f im Punkt S(0 |1) begrenzt mit den |
beiden Koordinatenachsen ein Dreieck. Weisen Sie nach, dass dieses | beiden Koordinatenachsen ein Dreieck. Weisen Sie nach, dass dieses | ||
Dreieck gleichschenklig ist. | Dreieck gleichschenklig ist. | ||
Version vom 29. Juni 2017, 11:11 Uhr
|
|
Gegeben ist die Funktion a) Geben Sie Dg und die Koordinaten des Schnittpunkts von Gg mit der y-Achse an. b) Beschreiben Sie, wie Gg schrittweise aus dem Graphen der in IR0+
definierten Funktion
|
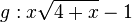 mit maximaler Definitionsmenge
Dg . Der Graph von g wird mit Gg bezeichnet.
mit maximaler Definitionsmenge
Dg . Der Graph von g wird mit Gg bezeichnet.
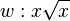 hervorgeht, und geben Sie die
Wertemenge von g an.
hervorgeht, und geben Sie die
Wertemenge von g an.

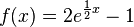 mit x ∈ IR gegeben.
mit x ∈ IR gegeben.


