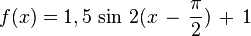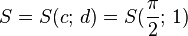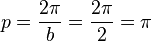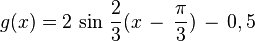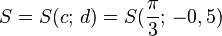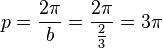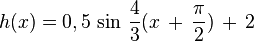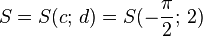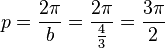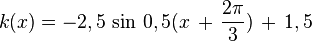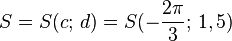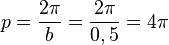Graph zeichnen: Unterschied zwischen den Versionen
Aus RMG-Wiki
(→Übungen zu y = a sin b(x - c) + d) |
(→Übungen zu y = a sin b(x - c) + d) |
||
| Zeile 5: | Zeile 5: | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| − | == | + | == y = a sin b(x - c) + d == |
Bewege die '''Punkte S ("Start"), P ("Periode") und B ("Berg")''' mit der Maus und '''zeichne so die Graphen der folgenden Funktionen'''!<br> | Bewege die '''Punkte S ("Start"), P ("Periode") und B ("Berg")''' mit der Maus und '''zeichne so die Graphen der folgenden Funktionen'''!<br> | ||
Du kanst Dein Ergebnis kontrollieren, wenn Du Dir den entsprechenden Graph anzeigen lässt.<br> | Du kanst Dein Ergebnis kontrollieren, wenn Du Dir den entsprechenden Graph anzeigen lässt.<br> | ||
Version vom 9. November 2014, 19:01 Uhr
y = a sin b(x - c) + dBewege die Punkte S ("Start"), P ("Periode") und B ("Berg") mit der Maus und zeichne so die Graphen der folgenden Funktionen!
|