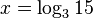Gleichungen: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
Zeile 1: Zeile 1:
 
__NOTOC__
 
__NOTOC__
−
<div style="padding:1px;background: #ABAABF;border:0px groove;">
+
<div style="background: #ABAABF">
−
<center><table border="0" width="1000px" cellpadding=2 cellspacing=2>
+
 
 +
<center><table border=0 width="800px" cellpadding=5 cellspacing=5>
 
<tr><td  width="800px" valign="top">
 
<tr><td  width="800px" valign="top">
  
 
{|
 
{|
−
|width="60%"|
+
|width="70%"|
 
== Teste dein Wissen ==
 
== Teste dein Wissen ==
 
<br/><br/><br/>
 
<br/><br/><br/>
Zeile 13: Zeile 14:
 
Ist das Ergebnis 0, trage "Null" ein. <br/>
 
Ist das Ergebnis 0, trage "Null" ein. <br/>
 
| type="{}" }
 
| type="{}" }
−
<math>4x+2=14 \qquad \qquad \qquad  x= </math>  { 3 } / { - } <br/><br/>
+
<math>4x+2=14 \qquad \qquad  x= </math>  { 3 } / { - } <br/><br/>
−
<math> -(x+1)=6-(3-x)\qquad  x=</math>    { -2 } /  { - }  <br/><br/>
+
<math> -(x+1)=6-(3-x) \quad x=</math>    { -2 } /  { - }  <br/><br/>
 
<math> 2x^2-30=68 \qquad \qquad x=</math>    { -7 }  /  { 7 }  <br/><br/>
 
<math> 2x^2-30=68 \qquad \qquad x=</math>    { -7 }  /  { 7 }  <br/><br/>
−
<math> 6x^2+66=72x\qquad\qquad  x=</math>    { 1 }  /  { 11 }  <br/><br/>
+
<math> 6x^2+66=72x\qquad x=</math>    { 1 }  /  { 11 }  <br/><br/>
 
<math> (x-4)(x- \frac 5 2)=0 \qquad x=</math> { -2,5 }  /  { 4 }  <br/><br/>
 
<math> (x-4)(x- \frac 5 2)=0 \qquad x=</math> { -2,5 }  /  { 4 }  <br/><br/>
 
<math> 56x+7x^2=0\qquad \qquad x=</math>    { -8 }  /  { Null }  <br/><br/>
 
<math> 56x+7x^2=0\qquad \qquad x=</math>    { -8 }  /  { Null }  <br/><br/>
Zeile 22: Zeile 23:
 
<math> x^4-3x^3=0 \qquad \qquad x=</math>    { Null }  /  { 2 }  <br/><br/>
 
<math> x^4-3x^3=0 \qquad \qquad x=</math>    { Null }  /  { 2 }  <br/><br/>
 
<math> \frac{15}{x-1}=\frac x 2  \qquad \qquad x=</math>    { -5 }  /  { 6 }  <br/><br/>
 
<math> \frac{15}{x-1}=\frac x 2  \qquad \qquad x=</math>    { -5 }  /  { 6 }  <br/><br/>
−
<math> 3^x=27 \qquad \qquad \qquad \qquad x=</math>    { 3 }  /  { - }  <br/><br/>
+
<math> 3^x=27 \qquad \qquad \qquad x=</math>    { 3 }  /  { - }  <br/><br/>
 
</quiz>
 
</quiz>
  
Zeile 35: Zeile 36:
 
== Knicktests ==  
 
== Knicktests ==  
 
<br/>  
 
<br/>  
−
[[Datei:2 AB0 Gleichungen S1.pdf|thumb|Knicktest - Einstieg Gleichungen S.1|300px|zentriert]]
+
[[Datei:2 AB0 Gleichungen S1.pdf|thumb|Knicktest - Einstieg Gleichungen S.1|zentriert]]
 
<br />
 
<br />
−
[[Datei:2 AB0 Gleichungen S2.pdf|thumb|Knicktest - Einstieg Gleichungen S.2|300px|zentriert]]
+
[[Datei:2 AB0 Gleichungen S2.pdf|thumb|Knicktest - Einstieg Gleichungen S.2|zentriert]]
 
<br />
 
<br />
−
[[Datei:2 AB1 GleichungenGemischt.pdf|thumb|Knicktest - Gleichungen|300px|zentriert]]<br />
+
[[Datei:2 AB1 GleichungenGemischt.pdf|thumb|Knicktest - Gleichungen|zentriert]]<br />
 
|}
 
|}
  
Zeile 69: Zeile 70:
 
<br/>  
 
<br/>  
 
<br/>  
 
<br/>  
−
 
+
[[Datei:2 AB2 Gleichungssysteme.pdf|thumb|Knicktest - Gleichungssysteme|zentriert]]
−
[[Datei:2 AB2 Gleichungssysteme.pdf|thumb|Knicktest - Gleichungssysteme|300px|zentriert]]
+
−
 
+
 
|}
 
|}
 +
 
[[Mathematik_Grundwissen_10|Zurück zur Übersicht]]
 
[[Mathematik_Grundwissen_10|Zurück zur Übersicht]]
 +
 +
</td></tr></table></center>
 +
</div>

Version vom 3. September 2014, 20:44 Uhr

Teste dein Wissen




1. Löse die folgenden Gleichungen. Achte auf die Anzahl der Lösungen.
Gibt es nur eine Lösungen, trage in das andere Feld "-" ein.
Gibt es zwei Lösungen, so ordne diese der Größe nach.
Ist das Ergebnis 0, trage "Null" ein.

4x+2=14 \qquad \qquad x= /

-(x+1)=6-(3-x) \quad x= /

2x^2-30=68 \qquad \qquad x= /

6x^2+66=72x\qquad x= /

(x-4)(x- \frac 5 2)=0 \qquad x= /

56x+7x^2=0\qquad \qquad x= /

x^5=64 \qquad \qquad \qquad x= /

x^4-3x^3=0 \qquad \qquad x= /

\frac{15}{x-1}=\frac x 2 \qquad \qquad x= /

3^x=27 \qquad \qquad \qquad x= /


Punkte: 0 / 0


3^x=15\qquad\qquad \qquad x=



Knicktests


Knicktest - Einstieg Gleichungen S.1


Knicktest - Einstieg Gleichungen S.2


Knicktest - Gleichungen



2a) Löse das folgende Gleichungssystem:

(Ι) 2x+2y=9
(ΙΙ) 1−6x=2y



2b) Markus kauft auf dem Weihnachtsmarkt drei Tassen Punsch und zwei Waffeln. Er zahlt dafür 8,50€. Uwe lädt seine Freunde ein und bestellt daher doppelt soviel Punsch als Markus, dazu eine Waffel. Er zahlt 2,50 € mehr als Markus. Nach dem Kauf überlegen die beiden, wie hoch der Preis für einen Punsch bzw. eine Waffel ist.
Stelle ein lineares Gleichungssystem auf, das ermöglicht diese Aufgabe zu lösen.




Knicktest - Gleichungssysteme

Zurück zur Übersicht

Von „http://rmg.zum.de/index.php?title=Mathematik_Grundwissen_10/Gleichungen&oldid=58379“