Gleichungen: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
Zeile 8: Zeile 8:
 
<math> 2x^2-30=68\qquad\qquad \qquad x=</math>    ''' -7 '''  /  ''' 7 '''  <br/>
 
<math> 2x^2-30=68\qquad\qquad \qquad x=</math>    ''' -7 '''  /  ''' 7 '''  <br/>
 
<math> 6x^2+66=72x\qquad\qquad \qquad x=</math>    ''' 1 '''  /  ''' 11 '''  <br/>
 
<math> 6x^2+66=72x\qquad\qquad \qquad x=</math>    ''' 1 '''  /  ''' 11 '''  <br/>
 +
übrige Lösungen:    ''' -3 '''  /  ''' 2 ''' /  ''' <math> \sqrt{19} </math>  ''' / ''' <math> - \sqrt{19} </math>  ''' /  ''' 6 ''' /  ''' -4 ''' /  ''' 2,5 '''/  ''' <math> \log_{15}{3}</math>  '''<br/>
 +
</div> <br/>
 +
<div class="lueckentext-quiz">
 
<math> (x-4)(x- \frac 5 2)=0\qquad\qquad \qquad x=</math>    ''' -2,5 '''  /  ''' 4 '''  <br/>
 
<math> (x-4)(x- \frac 5 2)=0\qquad\qquad \qquad x=</math>    ''' -2,5 '''  /  ''' 4 '''  <br/>
 
<math> 56x+7x^2=0\qquad\qquad \qquad x=</math>    ''' -8 '''  /  ''' 0 '''  <br/>
 
<math> 56x+7x^2=0\qquad\qquad \qquad x=</math>    ''' -8 '''  /  ''' 0 '''  <br/>
Zeile 18: Zeile 21:
 
übrige Lösungen:    ''' -3 '''  /  ''' 2 ''' /  ''' <math> \sqrt{19} </math>  ''' / ''' <math> - \sqrt{19} </math>  ''' /  ''' 6 ''' /  ''' -4 ''' /  ''' 2,5 '''/  ''' <math> \log_{15}{3}</math>  '''<br/>  
 
übrige Lösungen:    ''' -3 '''  /  ''' 2 ''' /  ''' <math> \sqrt{19} </math>  ''' / ''' <math> - \sqrt{19} </math>  ''' /  ''' 6 ''' /  ''' -4 ''' /  ''' 2,5 '''/  ''' <math> \log_{15}{3}</math>  '''<br/>  
 
</div> <br/>
 
</div> <br/>
 +
 +
 +
<quiz>
 +
{Löse die folgenden Gleichungen. Achte auf die Anzahl der Lösungen. <br/>Gibt es nur eine Lösungen, trage in das andere Feld "-" ein.<br/>
 +
Gibt es zwei Lösungen, so ordne diese der Größe nach.
 +
| type="{}" }
 +
<math>4x+2=14 \qquad \qquad \qquad  \qquad x= </math>  { 3 } ; { - } <br/>
 +
<math> -(x+1)=6-(3-x)\qquad \qquad\qquad x=</math>    { -2 } /  { - }  <br/>
 +
<math> 2x^2-30=68\qquad\qquad \qquad x=</math>    { -7 }  /  { 7 }  <br/>
 +
<math> 6x^2+66=72x\qquad\qquad \qquad x=</math>    { 1 }  /  { 11 }  <br/>
 +
</quiz>
 +
  
 
[[Mathematik_Grundwissen_10|Zurück zur Übersicht]]
 
[[Mathematik_Grundwissen_10|Zurück zur Übersicht]]

Version vom 1. September 2014, 20:00 Uhr

Teste dein Wissen


Löse die folgenden Gleichungen. Achte auf die Anzahl der Lösungen.
Gibt es nur eine Lösungen, trage in das andere Feld "-" ein.
Gibt es zwei Lösungen, so ordne diese der Größe nach.

4x+2=14 \qquad \qquad \qquad \qquad x= 3 / -
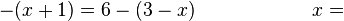-(x+1)=6-(3-x)\qquad \qquad\qquad x= -2 / -
2x^2-30=68\qquad\qquad \qquad x= -7 / 7
6x^2+66=72x\qquad\qquad \qquad x= 1 / 11
übrige Lösungen: -3 / 2 / 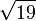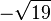\sqrt{19} / - \sqrt{19} / 6 / -4 / 2,5 /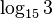 \log_{15}{3}


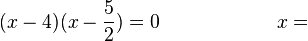(x-4)(x- \frac 5 2)=0\qquad\qquad \qquad x= -2,5 / 4
56x+7x^2=0\qquad\qquad \qquad x= -8 / 0
x^5=64\qquad\qquad \qquad x= 2 / -
x^4-3x^3=0\qquad\qquad \qquad x= 0 / 2
\frac{15}{x-1}=\frac x 2 \qquad\qquad \qquad x= -5 / 6
3^x=27\qquad\qquad \qquad x= 3 / -
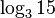3^x=15\qquad\qquad \qquad x= \log_{3}{15} / -

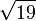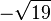übrige Lösungen: -3 / 2 / \sqrt{19} / - \sqrt{19} / 6 / -4 / 2,5 / \log_{15}{3}



Pluspunkt für eine richtige Antwort:  
Minuspunkte für eine falsche Antwort:
Ignoriere den Fragen-Koeffizienten:

1. Löse die folgenden Gleichungen. Achte auf die Anzahl der Lösungen.
Gibt es nur eine Lösungen, trage in das andere Feld "-" ein.
Gibt es zwei Lösungen, so ordne diese der Größe nach.

4x+2=14 \qquad \qquad \qquad \qquad x=  ;
-(x+1)=6-(3-x)\qquad \qquad\qquad x= /
2x^2-30=68\qquad\qquad \qquad x= /
6x^2+66=72x\qquad\qquad \qquad x= /

Punkte: 0 / 0


Zurück zur Übersicht

Von „http://rmg.zum.de/index.php?title=Mathematik_Grundwissen_10/Gleichungen&oldid=58335“