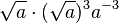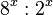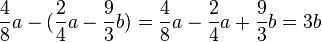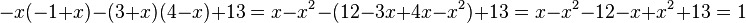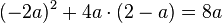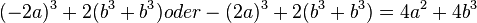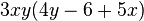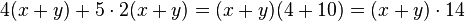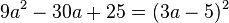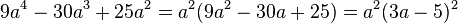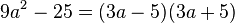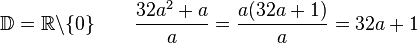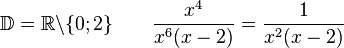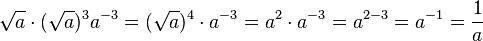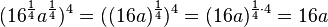Term und Zahl: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
Zeile 3: Zeile 3:
  
 
<br />
 
<br />
−
<quiz>
+
1.Vereinfache folgende Terme soweit wie möglich.
−
{1.Vereinfache folgende Terme soweit wie möglich.
+
 
−
| type="{}" }
+
<math>\frac48 a-(  \frac24 a- \frac93 b) =</math>
−
<math>\frac48 a-(  \frac24 a- \frac93 b) =</math> { 3b }
+
<popup name="Lösung">
−
<math> -x(-1-x)-(3+x)(4-x)+13=</math> { 1 }
+
<math>\frac48 a-(  \frac24 a- \frac93 b) =\frac48 a-  \frac24 a+ \frac93 b=3b </math>  
−
</quiz>
+
</popup> <br />
 +
 
 +
<math> -x(-1+x)-(3+x)(4-x)+13=</math>  
 +
<popup name="Lösung">
 +
<math> -x(-1+x)-(3+x)(4-x)+13=x-x^2-(12-3x+4x-x^2)+13=x-x^2-12-x+x^2+13=1</math>
 +
</popup> <br />
  
  

Version vom 23. Juli 2014, 19:10 Uhr

Teste dein Wissen


1.Vereinfache folgende Terme soweit wie möglich.

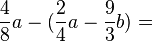
\frac48 a-( \frac24 a- \frac93 b) =


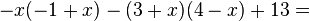
-x(-1+x)-(3+x)(4-x)+13=



2.Setze im ersten Term die Klammern so, dass eine richtige Termumformung entsteht.
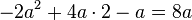
-2a^2+4a \cdot 2 - a = 8a


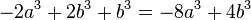
-2a^3+2b^3+b^3 = -8a^3+4b^3



3.Klammere den größtmöglichen Faktor aus.
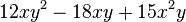
12xy^2-18xy+15x^2y


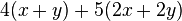
4(x+y)+5(2x+2y)



4.Faktorisiere den Term (mit Hilfe der binomischen Formeln)
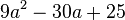
9a^2-30a+25


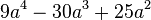
9a^4-30a^3+25a^2


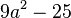
9a^2-25



5. Gib die Definitionsmenge an und vereinfache soweit wie möglich
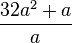
\frac{32a^2+a}{a}


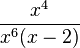
\frac{x^4}{x^6(x-2)}



6) Vereinfache soweit wie möglich (a>0)
\sqrt a \cdot (\sqrt a)^3 a^{-3}


(16^{\frac1 4} a^{\frac1 a})^4


8^x:2^x


Von „http://rmg.zum.de/index.php?title=Mathematik_Grundwissen_10/Term_und_Zahl&oldid=58272“