Benutzer:Karina Hetterich: Unterschied zwischen den Versionen
Aus RMG-Wiki
(→Terme und Zahlen) |
(→Teste dein Wissen) |
||
| Zeile 17: | Zeile 17: | ||
<math> -x(-1-x)-(3+x)(4-x)+12=</math> { "0" } | <math> -x(-1-x)-(3+x)(4-x)+12=</math> { "0" } | ||
</quiz> | </quiz> | ||
| − | Setze im ersten Term die Klammern so, dass eine richtige Termumformung entsteht <br /> | + | Setze im ersten Term die Klammern so, dass eine richtige Termumformung entsteht. <br /> |
<math>-2a^2+4a \cdot 2 - a = 8a</math> | <math>-2a^2+4a \cdot 2 - a = 8a</math> | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
| Zeile 26: | Zeile 26: | ||
<math>(-2a)^3+2(b^3+b^3) oder -(2a)^3+2(b^3+b^3) = 4a^2+4b^3 </math> | <math>(-2a)^3+2(b^3+b^3) oder -(2a)^3+2(b^3+b^3) = 4a^2+4b^3 </math> | ||
</popup> <br /> | </popup> <br /> | ||
| − | Klammere den größtmöglichen Faktor aus | + | Klammere den größtmöglichen Faktor aus.<br/> |
<math> 12xy^2-18xy+15x^2y</math> | <math> 12xy^2-18xy+15x^2y</math> | ||
<popup name = "Lösung"> | <popup name = "Lösung"> | ||
Version vom 20. Juni 2014, 09:00 Uhr
Teste dein WissenTerme und Zahlen
Setze im ersten Term die Klammern so, dass eine richtige Termumformung entsteht.
Klammere den größtmöglichen Faktor aus.
Gib die Definitionsmenge an und vereinfache soweit wie möglich
GleichungenLöse die folgenden Gleichungen. Achte auf die Anzahl der Lösungen.
|
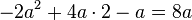
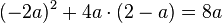
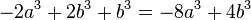
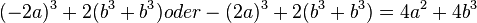
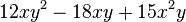
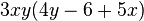
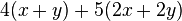
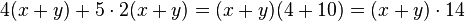
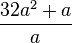
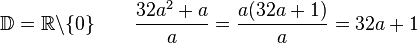
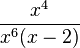
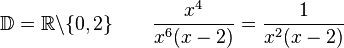
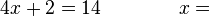 3 / -
3 / - 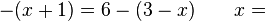 -2 / -
-2 / - 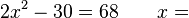 -7 / 7
-7 / 7 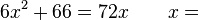 1 / 11
1 / 11 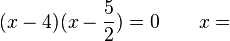 -2,5 / 4
-2,5 / 4 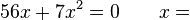 -8 / 0
-8 / 0 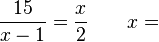 -5 / 6
-5 / 6 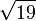 /
/ 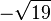 / 6 / -4 / 2,5
/ 6 / -4 / 2,5 
