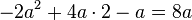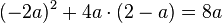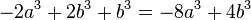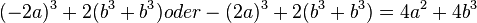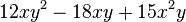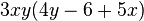Benutzer:Karina Hetterich: Unterschied zwischen den Versionen

Version vom 20. Juni 2014, 07:50 Uhr

Setze im ersten Term die Klammern so, dass eine richtige Termumformung entsteht
$-2a^2+4a \cdot 2 - a = 8a$

$-2a^3+2b^3+b^3 = -8a^3+4b^3$

Klammere den größtmöglichen Faktor aus $12xy^2-18xy+15x^2y$

@@ Zeile 17: / Zeile 17: @@
 <math> -x(-1-x)-(3+x)(4-x)+12=</math> { "0" }
 </quiz>
-Setze die Klammern so, dass eine richtige Termumformung entsteht
+Setze im ersten Term die Klammern so, dass eine richtige Termumformung entsteht <br />
 <math>-2a^2+4a \cdot 2 - a = 8a</math>
 <popup name="Lösung">
 <math>(-2a)^2+4a \cdot (2 - a) = 8a </math>
+</popup> <br />
+<math>-2a^3+2b^3+b^3 = -8a^3+4b^3</math>
+<popup name="Lösung">
+<math>(-2a)^3+2(b^3+b^3) oder -(2a)^3+2(b^3+b^3) = 4a^2+4b^3 </math>
 </popup> <br />
 Klammere den größtmöglichen Faktor aus