Mathematik - Seminare: Unterschied zwischen den Versionen
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 19: | Zeile 19: | ||
===<center><span style="color: darkblue; font-size:18pt;">'''W-Seminare'''</span></center>=== | ===<center><span style="color: darkblue; font-size:18pt;">'''W-Seminare'''</span></center>=== | ||
<br> | <br> | ||
| − | |||
| + | <span style="color: #CD0000; font-size:12pt;">'''Bedeutende Mathematiker von der Antike bis zur Gegenwart '''</span> | ||
| + | [[Datei:Kapitolinischer Pythagoras adjusted.jpg|80px|right]] | ||
| + | [[Datei:Carl Friedrich Gauss.jpg|80px|right]] | ||
| + | [[Datei:Andrew wiles1-3.jpg|80px|right]] | ||
:''Oberstufenjahrgang 2012/14, Leitung: StRin Schellmann'' | :''Oberstufenjahrgang 2012/14, Leitung: StRin Schellmann'' | ||
| Zeile 32: | Zeile 35: | ||
:Euklid von Alexandria und die Geometrie; Pythagoras von Samos und das rechtwinklige Dreieck; Leonhard Euler und die Zahl e; Carl Friedrich Gauß und die Glockenkurve; Regiomontanus und die Trigonometrie; Pierre-Simon Laplace und die Wahrscheinlichkeit; Der Weg der Emmy Noether... | :Euklid von Alexandria und die Geometrie; Pythagoras von Samos und das rechtwinklige Dreieck; Leonhard Euler und die Zahl e; Carl Friedrich Gauß und die Glockenkurve; Regiomontanus und die Trigonometrie; Pierre-Simon Laplace und die Wahrscheinlichkeit; Der Weg der Emmy Noether... | ||
| + | |||
| Zeile 37: | Zeile 41: | ||
:''Oberstufenjahrgang 2011/13, Leitung: StR Lehrl'' | :''Oberstufenjahrgang 2011/13, Leitung: StR Lehrl'' | ||
| − | + | [[Datei:Gaussplane kartesianAndPolar.png|200px|right]] | |
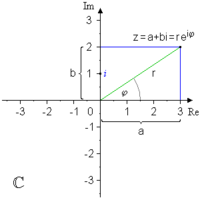
Welche Zahlenmengen gibt es? Warum wurden diese immer wieder erweitert? Bei einem Blick auf den in Unter- und Mittelstufe zurückgelegten Weg von den natürlichen bis zu den reellen Zahlen kristallisieren sich bereits wesentliche Prinzipien für Zahlenbereichserweiterungen heraus. In der Schule ist bei den reellen Zahlen Schluss, aber gibt es vielleicht noch eine größere Zahlenmenge, in der z.B. die Gleichung x<sup>2</sup> = -2 lösbar ist? | Welche Zahlenmengen gibt es? Warum wurden diese immer wieder erweitert? Bei einem Blick auf den in Unter- und Mittelstufe zurückgelegten Weg von den natürlichen bis zu den reellen Zahlen kristallisieren sich bereits wesentliche Prinzipien für Zahlenbereichserweiterungen heraus. In der Schule ist bei den reellen Zahlen Schluss, aber gibt es vielleicht noch eine größere Zahlenmenge, in der z.B. die Gleichung x<sup>2</sup> = -2 lösbar ist? | ||
| Zeile 48: | Zeile 52: | ||
:''Oberstufenjahrgang 2010/12, Leitung: StR Dietrich'' | :''Oberstufenjahrgang 2010/12, Leitung: StR Dietrich'' | ||
| − | + | [[Datei:Matheon2.jpg|200px|right]] | |
Die Mathematik ist eines der wichtigsten Werkzeuge zur Beschreibung der Natur. Nicht nur für die Physik und technikorientierten Studiengänge ist die „Sprache Mathematik“ unverzichtbar, auch z. B. die Chemie und die Biologie bedienen sich an vielen Stellen mathematischer Methoden. | Die Mathematik ist eines der wichtigsten Werkzeuge zur Beschreibung der Natur. Nicht nur für die Physik und technikorientierten Studiengänge ist die „Sprache Mathematik“ unverzichtbar, auch z. B. die Chemie und die Biologie bedienen sich an vielen Stellen mathematischer Methoden. | ||
| Zeile 60: | Zeile 64: | ||
:''Oberstufenjahrgang 2009/11, Leitung: StR Gramlich'' | :''Oberstufenjahrgang 2009/11, Leitung: StR Gramlich'' | ||
| − | + | [[Datei:Extrema example de.svg|200px|right]] | |
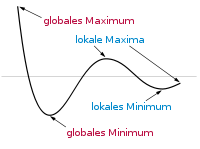
Wollen Sie Ihre Ziele mit dem geringstmöglichen Aufwand erreichen? | Wollen Sie Ihre Ziele mit dem geringstmöglichen Aufwand erreichen? | ||
Aktuelle Version vom 3. September 2012, 09:11 Uhr
|
|
|
|