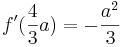Wendepunkt: Unterschied zwischen den Versionen
Aus RMG-Wiki
| (6 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | === | + | ===Bestimmung der größten Senkung der Durchflussgeschwindigkeit=== |
| − | '''''<span style="color: darkorange">Es soll | + | '''''<span style="color: darkorange">Es soll in Abhängigkeit von a bestimmt werden, wann die Druchflussgeschwindigkeit besonders stark absinkt. Dieser Wert soll zum Zeitpunkt t berechnet werden.</span> |
{| | {| | ||
| Zeile 12: | Zeile 12: | ||
| − | :''An dem erhaltenem Punkt besitzt der Graph G<sub>f</sub> den größten negativen Steigungswert. Dieser Punkt | + | :''An dem erhaltenem Punkt besitzt der Graph G<sub>f</sub> den größten negativen Steigungswert. Dieser Punkt ist ein möglicher Wendepunkt. An ihm ändert der Graph sein Krümmungsverhalten.'' |
| + | |||
| + | ::<span style="color: darkblue">Errechne die Koordinaten des möglichen Wendepunktes und überprüfe, ob es einer ist.</span> | ||
| + | |||
| + | ::'''<u><span style="color: red">Merke:</span></u>''' Es handelt sich nur um einen Wendepunkt, wenn folgende Kriterien erfüllt sind. | ||
| + | |||
| + | ::<math>\Rightarrow f''(t_0) = 0</math> | ||
| + | ::<math>\Rightarrow f'''(t_0) \neq 0</math><ref>[http://mathenexus.zum.de/html/analysis/kurvendiskussion/weiterfuehrendes/abl_05_zweiteAbl.htm Überprüfung des Wendepunkts]</ref> | ||
| + | |||
| − | |||
::{{Lösung versteckt|1= | ::{{Lösung versteckt|1= | ||
| Zeile 22: | Zeile 29: | ||
| − | |||
| + | ::Bei dem Punkt handelt es sich um einen Wendepunkt, da die dritte Ableitung <math>f'''(t) = \frac{3}{2} \Rightarrow f'''( \frac{4}{3}a ) = \frac{3}{2}</math> ungleich Null ist. | ||
| − | |||
| − | ::< | + | ::<u>Der Punkt, an welchem die Funktion besonders stark abfällt ist zugleich der Wendepunkt</u> <math>WP \left( \frac{4}{3}a / \frac{4}{27}a^3 \right)</math> |
| − | + | ||
}} | }} | ||
| Zeile 35: | Zeile 41: | ||
|valign="top" | | |valign="top" | | ||
Die '''<span style="color: blue">blaue Funktion zeigt die Ableitung f '(t)</span> der schwarzen Funktion f (t) für a = 3. | Die '''<span style="color: blue">blaue Funktion zeigt die Ableitung f '(t)</span> der schwarzen Funktion f (t) für a = 3. | ||
| − | <ggb_applet width=" | + | <ggb_applet width="320" height="363" version="3.2" ggbBase64="UEsDBBQACAAIALp4OzwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1VZNj9s2ED03v4LQKWmwtr4s24C9QZteFk2aw/YD6KEAJY0l1hSpktSunF/fISlpZSdbuEUO6cU0h8PhmzePI+7e9A0nD6A0k2IfRIswICAKWTJR7YPOHG42wZvbF7sKZAW5ouQgVUPNPkgWcWDtHbt98c1O1/KRUO5cfmXwuA8OlGsIiG4V0FLXAObMTruecUbV6UP+JxRGPy34IHei7fAUozq0FU35julxurQHHqQwhGj2ERB0bG27pcOyg67grGRU2PMcNnQi5JGVpkbYMSZYA6tqm0MW+WiFlKq8P2kDDel/ByX3QbpZbFbpOgvDLNpE4SrLAnLyS/EqXayyzTbN1vE6jberBPMsKEcocbZYr7M0XIVpsl1tt9EKdz2/5g6Hh3swBvnWhPagx6Qrxcr5/zv9veTlxFMrmTBvaWs65UqVDKZ7c7KHYZbKJvmdqDgMtgiZrKE45rK/98QlPvTPp9ZtcXDy6q3kUhFlE0X41TDmfnQ+FufkFTqf0HkMMWzQaT3axs7DjbkfnRdnwkMb8o7GpKNwPIZpYg0Y3CpspIPTHPg+eC8FNQHpBDPvvCUghhXHp3Ttpp+6Jkd5j3utww8oJioK8Ho/Pyr6/FGMc7wgIMiPXc6ODRhQX+Tk3fJCr7sjKAHcq1KgLDrZafJA+Vh5B7eEgjU49QsDn9TW+hfE5K0lVAoG/+FWebbdajhX/oV5txxBWAwa4RcGs8cMjE3P3l5TS2X/ldRYi713PV51bduIJ40gYOwlfYvjy/4V2RNMmSxJir/fkv6Pl8kifEVuSDLOYzt/TbZ+7nAAhwbwohsn0EMnHI6pKofgXEamRooFgtgHKFgzV7VrUNL1movSzljF9WdUjW2prSn+G/XC6QnUGZMu3HtZnvNLBdbJkYfNpbUBrDhagHJotiNK0mJId5NngK5IDQXkSfp8CeqhBLUvQXJegtiXIPNzT/41xNdXEJ98CeZd5/kauU8+Jf+MMrt7SpQ+T1cyBoz/10J1bUSTfvA9eQDk4z64SSckV+UPfwnvpH0vZU3LWcHMJd2FbBoqSiJog153AhuyRs4c08w+HggNXQeikS2Ap60z48JvIEpoO3EcAg/hPqmj+6ZOJZjt+udaPT1U5qXKUlcrO+R++K/VeuI7HfhOB76nL5p/Ddi3j9uYXNEsqqFZVL5Z3CRTX4iy6xpDdYXSx3fPv1b6+Bz5GpvyRXZzopfzb6h7pw5v6du/AVBLBwhCAv2anQMAAH0LAABQSwECFAAUAAgACAC6eDs8QgL9mp0DAAB9CwAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAANcDAAAAAA==" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> |
| + | |||
| + | <popup name="Berechnung der Steigung im Wendepunkt"> | ||
| + | :Um die Steigung zu bestimmen, welche der Graph im Wendepunkt besitzt, wird der t - Wert zusätzlich in die erste Ableitung <math> f_a '</math> eingesetzt. Der Wert, den man erhält ist die Steigung im Wendepunkt. Nun kann man noch die Wendetangente durch den Punkt aufstellen (siehe rote Linearfunktion im Applet). | ||
| + | |||
| + | :Diese lineare Funktion besitzt im Wendepunkt die Steigung | ||
| + | |||
| + | :<math>f' (\frac{4}{3}a) = - \frac{a^2}{3}</math> | ||
| + | </popup> | ||
|} | |} | ||
| − | [[ | + | [[LK Mathematik Abitur NRW 2007/Theoretische Überlegungen|Hier geht's zur Aufgabe: Theoretische Fragen zur Wasserstandsaufgabe]] |
| + | |||
| + | [[LK Mathematik Abitur NRW 2007|Hier geht's zurück zur Übersicht]] | ||
| − | + | ==Internetseiten== | |
| + | <references/> | ||
Aktuelle Version vom 6. Februar 2011, 15:54 Uhr
Bestimmung der größten Senkung der Durchflussgeschwindigkeit
Es soll in Abhängigkeit von a bestimmt werden, wann die Druchflussgeschwindigkeit besonders stark absinkt. Dieser Wert soll zum Zeitpunkt t berechnet werden.
|
Die blaue Funktion zeigt die Ableitung f '(t) der schwarzen Funktion f (t) für a = 3. |
Hier geht's zur Aufgabe: Theoretische Fragen zur Wasserstandsaufgabe
Hier geht's zurück zur Übersicht
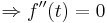
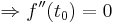
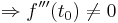
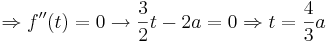
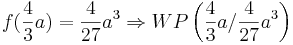
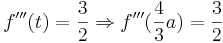 ungleich Null ist.
ungleich Null ist.
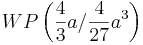
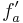 eingesetzt. Der Wert, den man erhält ist die Steigung im Wendepunkt. Nun kann man noch die Wendetangente durch den Punkt aufstellen (siehe rote Linearfunktion im Applet).
eingesetzt. Der Wert, den man erhält ist die Steigung im Wendepunkt. Nun kann man noch die Wendetangente durch den Punkt aufstellen (siehe rote Linearfunktion im Applet).