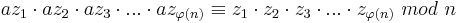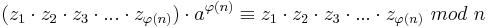Mathematische Grundlagen 3: Unterschied zwischen den Versionen
| (59 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | In der 6. Klasse hast du dich schon einmal mit Kehrwerten beschäftigt. Bei der Zahl 2 ist der Kehrwert bezüglich der Multiplikation 0,5. <math> 2\cdot 0,5 =1</math>, den Kehrwert kann man auch als Inverse bezeichnen. Im Folgenden gilt es zu untersuchen, ob auch modulare Inversen existieren und wenn ja unter welchen Bedingungen, wenn wir nur ganzzahlige Inverse betrachten möchten. | + | <div style="text-align:right;">[[Bild:Buch.PNG]][[Benutzer:Deininger_Matthias/Facharbeit/Fachwortverzeichnis| Fachwortverzeichnis]]</div> |
| + | ====Modulare Inverse==== | ||
| + | In der 6. Klasse hast du dich schon einmal mit Kehrwerten beschäftigt. Bei der Zahl 2 ist der Kehrwert bezüglich der Multiplikation 0,5. <math> 2\cdot 0,5 =1</math>, den Kehrwert kann man auch als multiplikative Inverse bezeichnen. Im Folgenden gilt es zu untersuchen, ob auch modulare Inversen existieren und, wenn ja, unter welchen Bedingungen, wenn wir nur ganzzahlige Inverse betrachten möchten. | ||
Aus den Angaben von Alice folgt: <math>a = 13, n = 24, x \in \Z</math> | Aus den Angaben von Alice folgt: <math>a = 13, n = 24, x \in \Z</math> | ||
Wie für den Kehrwert, so gilt auch für die modulare Inverse, dass das Resultat 1 ergeben muss.<br> | Wie für den Kehrwert, so gilt auch für die modulare Inverse, dass das Resultat 1 ergeben muss.<br> | ||
| + | <br> | ||
| + | <popup name="Definition der Inverse"> | ||
| + | Die Definition der Inverse findest du [http://de.wikipedia.org/wiki/Inverses_Element hier].<br> | ||
| + | <br> | ||
| + | <u>Das multiplikativ inverse Element:</u><br> | ||
| + | <br> | ||
| + | Als neutrales Element der Multiplikation wird 1 bezeichnet, weil <math>1 \cdot x\ =\ x</math>.<br> | ||
| + | Als multiplikativ inverses Element zu a wird <math>a^{-1}</math> bezeichnet, wenn gilt <math>a\cdot a^{-1}\ =\ 1</math> | ||
| + | <br> | ||
| + | </popup> | ||
<br> | <br> | ||
<table border="1" cellpadding="5" rules="all" style="text-align:center; color:black;margin:auto;font-size:12px; border:2px solid black;"> | <table border="1" cellpadding="5" rules="all" style="text-align:center; color:black;margin:auto;font-size:12px; border:2px solid black;"> | ||
| Zeile 15: | Zeile 27: | ||
</table> | </table> | ||
<br> | <br> | ||
| − | + | Diese Gleichungen sind äquivalent zu:<br> | |
| − | <math> | + | <math>a\cdot x = r\cdot n +1\ ;\ r\in\Z</math> |
| + | diese Schreibweise erinnert an [[Benutzer:Deininger_Matthias/Facharbeit/Mathematische_Grundlagen#Erweiterter_Euklidischer_Algorithmus|Lemma 1.4]], wonach man vermuten kann, dass die Gleichung nur für ggT(a,n) = 1 gilt. | ||
<br> | <br> | ||
| − | + | <br> | |
| − | <math> | + | Für die Aufgabe von Alice gilt somit:<br><br> |
| − | + | <math>13\cdot x\ mod\ 24 =1</math><br> | |
<br> | <br> | ||
<br> | <br> | ||
Falls eine Lösung existiert, soll nun eine ganze Zahl x gefunden werden, so dass die Gleichung erfüllt ist. | Falls eine Lösung existiert, soll nun eine ganze Zahl x gefunden werden, so dass die Gleichung erfüllt ist. | ||
| − | Wie du anhand von | + | Wie du anhand von Alices Beispiel selbst überprüfen kannst, ist dies bereits bei so kleinen Zahlen ziemlich schwierig. |
<br> | <br> | ||
| − | Deshalb betrachten wir nun den Satz von der modularen Inversen und werden darauf einen Algorithmus kennen lernen, mithilfe dessen sich die | + | Deshalb betrachten wir nun den Satz von der modularen Inversen und werden darauf einen Algorithmus kennen lernen, mithilfe dessen sich die modulo Inverse, die auch als multiplikative Inverse bezeichnet werden kann, relativ einfach berechnen lässt.<br> |
<br> | <br> | ||
| − | '''Satz 2.3'''<ref name=B3> | + | <div style = "border: 2px solid red; padding:0.75em;"> |
| + | '''Satz 2.3'''<ref name=B3>[2, S.107]</ref> (Satz von der modularen Inversen) Es sei <math>a,x \in \Z</math> und <math>n \in \N</math> mit ggT(a,n) = 1, so ist x die modulare Inverse zu a, wenn gilt:<br> | ||
<br> | <br> | ||
<math>a\cdot x\ mod\ n =1</math><br> | <math>a\cdot x\ mod\ n =1</math><br> | ||
| − | <br> | + | </div><br> |
| − | <u>Beweis:</u> Da gilt ggT(a,n)=1, gibt es ganze Zahlen x und y mit folgenden Eigenschaften:<br> | + | <popup name="Beweis"> |
| + | <u>Beweis:</u> Da gilt ggT(a,n) = 1, gibt es ganze Zahlen x und y mit folgenden Eigenschaften:<br> | ||
<math>1 =a\cdot x + n\cdot y</math><br> | <math>1 =a\cdot x + n\cdot y</math><br> | ||
da ny durch n teilbar ist, ergibt ax bei Division durch n den Rest 1, also ist<br> | da ny durch n teilbar ist, ergibt ax bei Division durch n den Rest 1, also ist<br> | ||
<math>a\cdot x\ mod\ n =1</math><br> | <math>a\cdot x\ mod\ n =1</math><br> | ||
<br> | <br> | ||
| − | Folglich gibt es immer eine eindeutige modulare Inverse, wenn gilt ggT(a,n)=1 □<br> | + | Folglich gibt es immer eine eindeutige modulare Inverse, wenn gilt ggT(a,n) = 1 □<br> |
| + | </popup> | ||
<br> | <br> | ||
| − | Wie du bereits aus Abschnitt 1 weißt, lässt sich der ggT zweier Zahlen mithilfe des Euklidischen Algorithmus bestimmen. <br> | + | Wie du bereits aus Abschnitt 1 weißt, lässt sich der ggT zweier Zahlen mithilfe des [[Benutzer:Deininger_Matthias/Facharbeit/Mathematische_Grundlagen#Euklidischer_Algorithmus|Euklidischen Algorithmus]] bestimmen. <br> |
<br> | <br> | ||
| + | <div style = "border: 2px solid red; padding:0.75em;"> | ||
'''Algorithmus 2.4'''<ref name=B3 /> (Berechnung der modularen Inverse) | '''Algorithmus 2.4'''<ref name=B3 /> (Berechnung der modularen Inverse) | ||
Es seien <math>a,n \in \Z</math> mit ggT(a,n) = 1. | Es seien <math>a,n \in \Z</math> mit ggT(a,n) = 1. | ||
Man berechne zunächst die Vielfachsummendarstellung <math>1=a\cdot x+y\cdot n</math>. Dann ist x die modulare Inverse von a modulo n.<br> | Man berechne zunächst die Vielfachsummendarstellung <math>1=a\cdot x+y\cdot n</math>. Dann ist x die modulare Inverse von a modulo n.<br> | ||
| + | </div><br> | ||
| + | Bei den von Alice gewählten Zahlen gilt ggT(13,24) = 1, also existiert eine modulare Inverse, da <math>13,24 \in\Z</math> lässt sich obiger Algorithmus hier anwenden, um die modulare Inverse zu 13 mod 24 zu bestimmen.<br> | ||
| + | Gesucht sind x und y, für die gilt: <math>x,y \in \Z</math><br> | ||
| + | 1 = 13x + 24y<br> | ||
| + | <div style = "background-color: #BEFF9E;padding: 5px;border: 2px solid #E5CC00;border-color: green;"> | ||
| + | <u>Aufgabe:</u><br> | ||
<br> | <br> | ||
| − | + | Bestimme mithilfe des ''Euklidischen Algorithmus'' die Vielfachsummendarstellung von 13 und 24 und ermittle daraus die modulare Inverse zu 13 mod 24.</div><br> | |
| − | + | ||
| − | + | ||
| − | Bestimme mithilfe des Euklidischen Algorithmus die Vielfachsummendarstellung von 13 und 24 und ermittle daraus die modulare Inverse zu 13 mod 24.< | + | |
| − | <br> | + | |
<popup name="Lösung"> | <popup name="Lösung"> | ||
<br> | <br> | ||
| Zeile 73: | Zeile 92: | ||
<math>=> ggT(13,24)=\ 1</math><br><br> | <math>=> ggT(13,24)=\ 1</math><br><br> | ||
| − | + | Vielfachsummendarstellung:<br> | |
<math>1= 2-1\cdot 1 = 2-1\cdot (11-5\cdot 2)= 6\cdot 2-1\cdot 11 =</math><br> | <math>1= 2-1\cdot 1 = 2-1\cdot (11-5\cdot 2)= 6\cdot 2-1\cdot 11 =</math><br> | ||
<math>\quad\ = (13-11)\cdot 6-1\cdot 11=13\cdot 6-7\cdot 11=</math><br> | <math>\quad\ = (13-11)\cdot 6-1\cdot 11=13\cdot 6-7\cdot 11=</math><br> | ||
| Zeile 83: | Zeile 102: | ||
</popup> | </popup> | ||
<br> | <br> | ||
| − | Alice beschäftigt sich jetzt mit dem Satz von | + | Alice beschäftigt sich jetzt mit dem Satz von Fermat, sowie dem Satz von Euler, weil sie gelesen hat, dass diese Sätze elementar für das [[Benutzer:Deininger_Matthias/Facharbeit/RSA-Kryptosystem| RSA-Kryptosystem ]] sind. Folglich solltest auch du diese beiden Sätze kennenlernen, bevor du dich dem [[Benutzer:Deininger_Matthias/Facharbeit/RSA-Kryptosystem| RSA-Kryptosystem ]] zuwendest.<br> |
<br> | <br> | ||
| − | + | ====Kleiner Satz von Fermat==== | |
| − | + | ||
<br> | <br> | ||
| − | <math>a | + | <div style = "border: 2px solid red; padding:0.75em;"> |
| + | '''Satz 2.5'''<ref name=S12>Satz 2.5, der zugehörige Beweis und Satz 2.6 wurden [10, S.5] entnommen. Der Beweis zu Satz 2.6 wurde analog zum Beweis von Satz 2.5 entwickelt.</ref> (Der kleine Satz von Fermat) Es sei p eine Primzahl, so gilt für alle <math>a \in \Z</math> | ||
| + | mit ggT(a,p) = 1: <br> | ||
<br> | <br> | ||
| + | <math>a^{p-1}\equiv 1\ mod\ p</math><br> | ||
| + | </div><br> | ||
| + | <popup name="Beweis"> | ||
<u>Beweis:</u> (durch Betrachtung der Äquivalenzklassen/Restklassenrepräsentanten)<br> | <u>Beweis:</u> (durch Betrachtung der Äquivalenzklassen/Restklassenrepräsentanten)<br> | ||
Die möglichen Reste ungleich 0 bei Division einer ganzen Zahl durch p sind 1,2,3, ... ,p-1. Die Zahlen <math>1\cdot a, 2\cdot a, 3\cdot a, ...,(p-1)\cdot a</math> sind ebenfalls (p-1) verschiedene Zahlen; je zwei von ihnen haben verschiedene Reste (ungleich 0) mod p, da wegen ggT(a,p) = 1 gilt: | Die möglichen Reste ungleich 0 bei Division einer ganzen Zahl durch p sind 1,2,3, ... ,p-1. Die Zahlen <math>1\cdot a, 2\cdot a, 3\cdot a, ...,(p-1)\cdot a</math> sind ebenfalls (p-1) verschiedene Zahlen; je zwei von ihnen haben verschiedene Reste (ungleich 0) mod p, da wegen ggT(a,p) = 1 gilt: | ||
| − | <math>k\cdot a \equiv l\cdot a\ (mod\ p) \Rightarrow k \equiv l\ | + | <math>k\cdot a \equiv l\cdot a\ (mod\ p) \Rightarrow k \equiv l\ mod\ p</math>, |
| − | + | was wegen der Größe dieser Zahlen nur für k = l möglich ist. Also ist jede der Zahlen <math>i\cdot a</math> | |
kongruent zu genau einem Element aus {1,2,3, ... ,p-1} und es gilt:<br> | kongruent zu genau einem Element aus {1,2,3, ... ,p-1} und es gilt:<br> | ||
<br> | <br> | ||
<math>[1\cdot a], [2\cdot a], [3\cdot a], ..., [(p-1)\cdot a] = [1],[2],[3],..., [p-1] d.h. </math><br> | <math>[1\cdot a], [2\cdot a], [3\cdot a], ..., [(p-1)\cdot a] = [1],[2],[3],..., [p-1] d.h. </math><br> | ||
| − | <math>\{(1\cdot 2\cdot 3\cdot ...\cdot (p-1)) \cdot a^{p-1}\} \equiv \{1\cdot 2\cdot 3\cdot ... \cdot (p-1)]\}\ | + | <math>\{(1\cdot 2\cdot 3\cdot ...\cdot (p-1)) \cdot a^{p-1}\} \equiv \{1\cdot 2\cdot 3\cdot ... \cdot (p-1)]\}\ mod\ p</math> <br> |
<br> | <br> | ||
| − | + | Hieraus folgt durch Division: <math>a^{p-1} \equiv 1\ mod\ p</math> □ <br> | |
| + | </popup> | ||
<br> | <br> | ||
Alice wählt sich p = 5 und a = 4, um den Satz zu testen.<br> | Alice wählt sich p = 5 und a = 4, um den Satz zu testen.<br> | ||
Somit gilt nach dem kleinen Satz von Fermat:<br> | Somit gilt nach dem kleinen Satz von Fermat:<br> | ||
| − | + | <math>4^4\ mod\ 5 = 256\ mod\ 5 = 1</math> <br> | |
<br> | <br> | ||
Beim Satz von Fermat handelt es sich lediglich um einen Sonderfall des Satzes von Euler:<br> | Beim Satz von Fermat handelt es sich lediglich um einen Sonderfall des Satzes von Euler:<br> | ||
| + | ====Satz von Euler==== | ||
<br> | <br> | ||
| − | '''Satz 2.6'''<ref name=S12 /> (Satz von Euler) Es sei n | + | <div style = "border: 2px solid red; padding:0.75em;">'''Satz 2.6'''<ref name=S12 /> (Satz von Euler) Es sei <math>n \in \N</math>, so gilt für jedes a mit ggT(a,n) = 1: |
| − | + | ||
| − | + | ||
<br> | <br> | ||
| + | <math>a^{\varphi(n)} \equiv 1\ mod\ n</math><br> | ||
| + | </div><br> | ||
Hierbei bezeichnet <math>\varphi(n)</math> die Anzahl der zu n teilerfremden Zahlen aus der Menge {1,2,...,n-1}. Wenn p eine Primzahl ist, so gilt: <math>\varphi(p)= p-1</math>, für zwei voneinander verschiedene Primzahlen p,q gilt folglich: <math>\varphi(p\cdot q)=(p-1)\cdot (q-1)</math><br> | Hierbei bezeichnet <math>\varphi(n)</math> die Anzahl der zu n teilerfremden Zahlen aus der Menge {1,2,...,n-1}. Wenn p eine Primzahl ist, so gilt: <math>\varphi(p)= p-1</math>, für zwei voneinander verschiedene Primzahlen p,q gilt folglich: <math>\varphi(p\cdot q)=(p-1)\cdot (q-1)</math><br> | ||
<br> | <br> | ||
<popup name="Beweis"> | <popup name="Beweis"> | ||
<br> | <br> | ||
| + | <u>Beweis:</u><br> | ||
| + | Es bezeichnet <math>\varphi(n)</math> die eulersche <math>\varphi-Funktion</math>, die zu einer Zahl <math>n \in \N</math> die entsprechende Anzahl der zu n teilerfremden Zahlen angibt, wobei <math>z_k\ </math> die <math>\varphi(n)</math> verschiedenen Repräsentanten dieser Restklasse bezeichnen.<br> | ||
| + | <br> | ||
| + | Da <math>a\cdot z_i\ \not\equiv \ a\cdot z_j\ mod\ n</math> für <math>i \ne j</math>, ist es möglich einen Repräsentanten <math>z_l\ </math> mit dem konstanten Faktor a zu multiplizieren und dabei erneut Repräsentanten der Restklasse zu erhalten.<br> | ||
| + | <br> | ||
| + | Daher muss gelten: | ||
| + | <br> | ||
| + | <br><math>az_1\cdot az_2\cdot az_3\cdot...\cdot az_{\varphi(n)} \equiv z_1\cdot z_2\cdot z_3\cdot...\cdot z_{\varphi(n)} \ mod\ n</math><br> | ||
| + | <br><math>( z_1\cdot z_2\cdot z_3\cdot...\cdot z_{\varphi(n)} ) \cdot a^{\varphi(n)} \equiv z_1\cdot z_2\cdot z_3\cdot...\cdot z_{\varphi(n)}\ mod\ n</math><br> | ||
| + | Hieraus folgt somit:<br> | ||
| + | <br> | ||
| + | <math>a^{\varphi(n)} \equiv 1\ mod\ n</math> □ <br> | ||
| + | |||
| + | |||
| + | |||
</popup> | </popup> | ||
<br> | <br> | ||
| − | [[Benutzer:Deininger_Matthias/Facharbeit/RSA-Algorithmus| ''' | + | [[Bild:Weiter.png|weiter]] [[Benutzer:Deininger_Matthias/Facharbeit/RSA-Algorithmus| '''weiter zum RSA-Algorithmus''']] |
<br> | <br> | ||
<br> | <br> | ||
| + | [[Benutzer:Deininger_Matthias/Facharbeit| zurück zur Übersicht]] | ||
---- | ---- | ||
<references /> | <references /> | ||
[[Benutzer:Deininger_Matthias/Facharbeit/Literaturverzeichnis| siehe dazu Literaturverzeichnis]] | [[Benutzer:Deininger_Matthias/Facharbeit/Literaturverzeichnis| siehe dazu Literaturverzeichnis]] | ||
Aktuelle Version vom 23. Dezember 2010, 09:00 Uhr
Modulare Inverse
In der 6. Klasse hast du dich schon einmal mit Kehrwerten beschäftigt. Bei der Zahl 2 ist der Kehrwert bezüglich der Multiplikation 0,5. 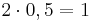 , den Kehrwert kann man auch als multiplikative Inverse bezeichnen. Im Folgenden gilt es zu untersuchen, ob auch modulare Inversen existieren und, wenn ja, unter welchen Bedingungen, wenn wir nur ganzzahlige Inverse betrachten möchten.
Aus den Angaben von Alice folgt:
, den Kehrwert kann man auch als multiplikative Inverse bezeichnen. Im Folgenden gilt es zu untersuchen, ob auch modulare Inversen existieren und, wenn ja, unter welchen Bedingungen, wenn wir nur ganzzahlige Inverse betrachten möchten.
Aus den Angaben von Alice folgt: 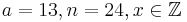 Wie für den Kehrwert, so gilt auch für die modulare Inverse, dass das Resultat 1 ergeben muss.
Wie für den Kehrwert, so gilt auch für die modulare Inverse, dass das Resultat 1 ergeben muss.
| Allgemein gilt also: | Alternative Schreibweise für die modulare Inverse: |
|---|---|
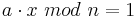 |
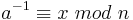 |
Diese Gleichungen sind äquivalent zu:
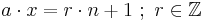 diese Schreibweise erinnert an Lemma 1.4, wonach man vermuten kann, dass die Gleichung nur für ggT(a,n) = 1 gilt.
diese Schreibweise erinnert an Lemma 1.4, wonach man vermuten kann, dass die Gleichung nur für ggT(a,n) = 1 gilt.
Für die Aufgabe von Alice gilt somit:
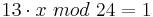
Falls eine Lösung existiert, soll nun eine ganze Zahl x gefunden werden, so dass die Gleichung erfüllt ist.
Wie du anhand von Alices Beispiel selbst überprüfen kannst, ist dies bereits bei so kleinen Zahlen ziemlich schwierig.
Deshalb betrachten wir nun den Satz von der modularen Inversen und werden darauf einen Algorithmus kennen lernen, mithilfe dessen sich die modulo Inverse, die auch als multiplikative Inverse bezeichnet werden kann, relativ einfach berechnen lässt.
Satz 2.3[1] (Satz von der modularen Inversen) Es sei 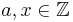 und
und 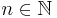 mit ggT(a,n) = 1, so ist x die modulare Inverse zu a, wenn gilt:
mit ggT(a,n) = 1, so ist x die modulare Inverse zu a, wenn gilt:
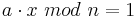
Wie du bereits aus Abschnitt 1 weißt, lässt sich der ggT zweier Zahlen mithilfe des Euklidischen Algorithmus bestimmen.
Algorithmus 2.4[1] (Berechnung der modularen Inverse)
Es seien 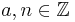 mit ggT(a,n) = 1.
Man berechne zunächst die Vielfachsummendarstellung
mit ggT(a,n) = 1.
Man berechne zunächst die Vielfachsummendarstellung 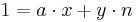 . Dann ist x die modulare Inverse von a modulo n.
. Dann ist x die modulare Inverse von a modulo n.
Bei den von Alice gewählten Zahlen gilt ggT(13,24) = 1, also existiert eine modulare Inverse, da 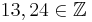 lässt sich obiger Algorithmus hier anwenden, um die modulare Inverse zu 13 mod 24 zu bestimmen.
lässt sich obiger Algorithmus hier anwenden, um die modulare Inverse zu 13 mod 24 zu bestimmen.
Gesucht sind x und y, für die gilt: 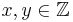
1 = 13x + 24y
Aufgabe:
Alice beschäftigt sich jetzt mit dem Satz von Fermat, sowie dem Satz von Euler, weil sie gelesen hat, dass diese Sätze elementar für das RSA-Kryptosystem sind. Folglich solltest auch du diese beiden Sätze kennenlernen, bevor du dich dem RSA-Kryptosystem zuwendest.
Kleiner Satz von Fermat
Satz 2.5[2] (Der kleine Satz von Fermat) Es sei p eine Primzahl, so gilt für alle 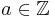 mit ggT(a,p) = 1:
mit ggT(a,p) = 1:
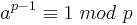
Alice wählt sich p = 5 und a = 4, um den Satz zu testen.
Somit gilt nach dem kleinen Satz von Fermat:
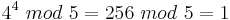
Beim Satz von Fermat handelt es sich lediglich um einen Sonderfall des Satzes von Euler:
Satz von Euler
Hierbei bezeichnet 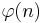 die Anzahl der zu n teilerfremden Zahlen aus der Menge {1,2,...,n-1}. Wenn p eine Primzahl ist, so gilt:
die Anzahl der zu n teilerfremden Zahlen aus der Menge {1,2,...,n-1}. Wenn p eine Primzahl ist, so gilt: 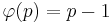 , für zwei voneinander verschiedene Primzahlen p,q gilt folglich:
, für zwei voneinander verschiedene Primzahlen p,q gilt folglich: 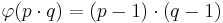
![]() weiter zum RSA-Algorithmus
weiter zum RSA-Algorithmus
zurück zur Übersicht
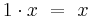 .
.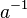 bezeichnet, wenn gilt
bezeichnet, wenn gilt 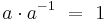
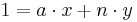
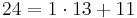
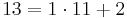
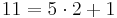
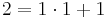
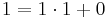
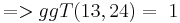
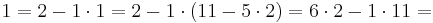
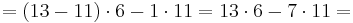
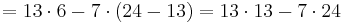
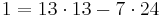
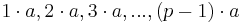 sind ebenfalls (p-1) verschiedene Zahlen; je zwei von ihnen haben verschiedene Reste (ungleich 0) mod p, da wegen ggT(a,p) = 1 gilt:
sind ebenfalls (p-1) verschiedene Zahlen; je zwei von ihnen haben verschiedene Reste (ungleich 0) mod p, da wegen ggT(a,p) = 1 gilt:
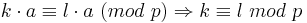 ,
was wegen der Größe dieser Zahlen nur für k = l möglich ist. Also ist jede der Zahlen
,
was wegen der Größe dieser Zahlen nur für k = l möglich ist. Also ist jede der Zahlen 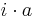 kongruent zu genau einem Element aus {1,2,3, ... ,p-1} und es gilt:
kongruent zu genau einem Element aus {1,2,3, ... ,p-1} und es gilt:![[1\cdot a], [2\cdot a], [3\cdot a], ..., [(p-1)\cdot a] = [1],[2],[3],..., [p-1] d.h.](/images/math/1/b/f/1bfde9c09eee176ba8429a03e6569cb8.png)
![\{(1\cdot 2\cdot 3\cdot ...\cdot (p-1)) \cdot a^{p-1}\} \equiv \{1\cdot 2\cdot 3\cdot ... \cdot (p-1)]\}\ mod\ p](/images/math/f/7/f/f7f72bbe1b69cd72a71b6915ee0ae05a.png)
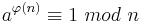
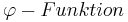 , die zu einer Zahl
, die zu einer Zahl 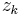 die
die 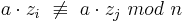 für
für 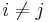 , ist es möglich einen Repräsentanten
, ist es möglich einen Repräsentanten 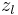 mit dem konstanten Faktor a zu multiplizieren und dabei erneut Repräsentanten der Restklasse zu erhalten.
mit dem konstanten Faktor a zu multiplizieren und dabei erneut Repräsentanten der Restklasse zu erhalten.