RSA-Signaturverfahren: Unterschied zwischen den Versionen
| (17 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <div style="text-align:right;">[[Bild:Buch.PNG]][[Benutzer:Deininger_Matthias/Facharbeit/Fachwortverzeichnis| Fachwortverzeichnis]]</div> | ||
===RSA-Signaturverfahren=== | ===RSA-Signaturverfahren=== | ||
<br> | <br> | ||
| Zeile 5: | Zeile 6: | ||
Um das zu verhindern, sollten Alice und Bob die Nachricht signieren, was einer Umkehrung der RSA-Verschlüsselung gleich kommt.<br> | Um das zu verhindern, sollten Alice und Bob die Nachricht signieren, was einer Umkehrung der RSA-Verschlüsselung gleich kommt.<br> | ||
<br> | <br> | ||
| − | '''Algorithmus 4.0'''<ref>[12, S.71]</ref>(RSA-Public-Key-Signaturverfahren)<br> | + | <div style = "text-align: left; padding:10px; width: 500px; height: 205px; border: 2px solid #E5CC00;border-color: orange;">'''Algorithmus 4.0'''<ref>[12, S.71]</ref>(RSA-Public-Key-Signaturverfahren)<br> |
(1) Zur Signierung führt Alice die folgenden Schritte aus:<br> | (1) Zur Signierung führt Alice die folgenden Schritte aus:<br> | ||
:(a) Alice berechnet die Signatur: <math>sig = m^d\ mod\ n</math> <br> | :(a) Alice berechnet die Signatur: <math>sig = m^d\ mod\ n</math> <br> | ||
| Zeile 11: | Zeile 12: | ||
(2) Zur Verifizierung und zum Erhalt der Nachricht führt Bob die folgenden Schritte aus:<br> | (2) Zur Verifizierung und zum Erhalt der Nachricht führt Bob die folgenden Schritte aus:<br> | ||
:(a) Bob besorgt sich den authentischen öffentlichen Schlüssel (n, e) von Alice.<br> | :(a) Bob besorgt sich den authentischen öffentlichen Schlüssel (n, e) von Alice.<br> | ||
| − | :(b) Bob berechnet <math>m = sig^e\ mod\ n</math>. Wenn <math>sig^e\ mod\ n</math> kein plausibler Klartext ist, wird die Signatur abgelehnt, andernfalls wird sie akzeptiert und <math>sig^e\ mod\ n</math> als m anerkannt.< | + | :(b) Bob berechnet <math>m = sig^e\ mod\ n</math>. Wenn <math>sig^e\ mod\ n</math> kein plausibler Klartext ist, wird die Signatur abgelehnt, andernfalls wird sie akzeptiert und <math>sig^e\ mod\ n</math> als m anerkannt.</div><br> |
| − | <br> | + | |
Wenn man das Signaturprotokoll so anwendet, wie es oben beschrieben ist, ergibt sich das Problem, dass die Signatur die gleiche Länge besitzt, wie das zu unterzeichnende Dokument, was auch bedeutet, dass ein ziemlich hoher Zeitbedarf zur Signierung nötig ist. | Wenn man das Signaturprotokoll so anwendet, wie es oben beschrieben ist, ergibt sich das Problem, dass die Signatur die gleiche Länge besitzt, wie das zu unterzeichnende Dokument, was auch bedeutet, dass ein ziemlich hoher Zeitbedarf zur Signierung nötig ist. | ||
Der Vorteil bei dem Verfahren ist jedoch, dass sogenanntes „Message Recovery“ besteht. Dies bedeutet, dass die Originalnachricht bei der Verifizierung aus der Signatur wieder gewonnen werden kann.<br> | Der Vorteil bei dem Verfahren ist jedoch, dass sogenanntes „Message Recovery“ besteht. Dies bedeutet, dass die Originalnachricht bei der Verifizierung aus der Signatur wieder gewonnen werden kann.<br> | ||
| Zeile 21: | Zeile 21: | ||
RSA wird gewöhnlich in Blöcken verschlüsselt, da für die Nachricht m gelten muss m < n. Mallory hat daher unter Umständen die Möglichkeit, einzelne Blöcke der Signatur zu entfernen, so dass sich beim Entschlüsseln dennoch ein sinnvoller, vermutlich aber sinnentstellter Text ergibt. Der Angriff ist also noch nicht abgewehrt.<br> | RSA wird gewöhnlich in Blöcken verschlüsselt, da für die Nachricht m gelten muss m < n. Mallory hat daher unter Umständen die Möglichkeit, einzelne Blöcke der Signatur zu entfernen, so dass sich beim Entschlüsseln dennoch ein sinnvoller, vermutlich aber sinnentstellter Text ergibt. Der Angriff ist also noch nicht abgewehrt.<br> | ||
<br> | <br> | ||
| − | Eine mögliche Lösung für das Problem besteht in der Verwendung von sog. [[Benutzer:Deininger_Matthias/Facharbeit/Hashfunktion| | + | Eine mögliche Lösung für das Problem besteht in der Verwendung von sog. [[Benutzer:Deininger_Matthias/Facharbeit/Hashfunktion| Hashfunktionen]] H(m), mit deren Hilfe es möglich ist, Nachrichten nahezu beliebiger Länge auf eine durch die [[Benutzer:Deininger_Matthias/Facharbeit/Hashfunktion| Hashfunktion]] festgelegte Größe zusammenzufassen. Dieses Zusammenfassen kann auch als „message digest“ bezeichnet werden.<br> |
<math>H(m) = h\ </math><br> | <math>H(m) = h\ </math><br> | ||
| − | Anschließend sollte der gebildete Hashwert, also die gehashte Nachricht mit oben beschriebenem Protokoll signiert werden, was dank der Kürze der kryptographischen Prüfsumme meist deutlich schneller möglich ist und überdies noch Speicherplatz spart. Dieses | + | Anschließend sollte der gebildete Hashwert h, also die gehashte Nachricht mit oben beschriebenem Protokoll signiert werden, was dank der Kürze der kryptographischen Prüfsumme meist deutlich schneller möglich ist und überdies noch Speicherplatz spart. Dieses |
Vorgehen kann man als Hash-and-Sign-Verfahren bezeichnen.<br> | Vorgehen kann man als Hash-and-Sign-Verfahren bezeichnen.<br> | ||
<br> | <br> | ||
| − | Wichtig ist hierbei zu erwähnen, dass es sich bei [[Benutzer:Deininger_Matthias/Facharbeit/Hashfunktion| | + | Wichtig ist hierbei zu erwähnen, dass es sich bei [[Benutzer:Deininger_Matthias/Facharbeit/Hashfunktion| Hashfunktionen]] vermutlich um [[Benutzer:Deininger_Matthias/Facharbeit/Einwegfunktion |Einwegfunktionen]] handelt, die nicht effizient umkehrbar sind. <br> |
<br> | <br> | ||
Folglich sollte Alice neben dem signierten Hashwert auch die ursprüngliche Nachricht (Urbild) an Bob senden. <br> | Folglich sollte Alice neben dem signierten Hashwert auch die ursprüngliche Nachricht (Urbild) an Bob senden. <br> | ||
<br> | <br> | ||
| − | Nach dem Erhalt der Nachricht von Alice empfiehlt es sich für Bob zunächst die Signatur von Alice zu verifizieren. Dazu kann Bob die Signatur mit Alices öffentlichem Schlüssel dechiffrieren, worauf er den Signaturhashwert erhält. Um zu überprüfen, ob die Originalnachricht oder die Signatur von Mallory verändert wurde, hat er die Möglichkeit, aus dem unverschlüsselten Klartext ebenfalls einen Hashwert zu bilden. Dazu sollte Bob, um ein verwertbares Ergebnis zu erhalten, die gleiche [[Benutzer:Deininger_Matthias/Facharbeit/Hashfunktion| Hashfunktion]], die auch Alice verwendet hat, anwenden. Die Information, welche [[Benutzer:Deininger_Matthias/Facharbeit/Hashfunktion| Hashfunktion]] von Alice verwendet wurde, ist in der Regel neben dem Hashwert in der Signatur enthalten. Anschließend kann Bob die Hashwerte vergleichen. Stimmen sie überein, wurde nichts verändert.<br> | + | Nach dem Erhalt der Nachricht von Alice, empfiehlt es sich für Bob, zunächst die Signatur von Alice zu verifizieren. Dazu kann Bob die Signatur mit Alices öffentlichem Schlüssel dechiffrieren, worauf er den Signaturhashwert erhält. Um zu überprüfen, ob die Originalnachricht oder die Signatur von Mallory verändert wurde, hat er die Möglichkeit, aus dem unverschlüsselten Klartext ebenfalls einen Hashwert zu bilden. Dazu sollte Bob, um ein verwertbares Ergebnis zu erhalten, die gleiche [[Benutzer:Deininger_Matthias/Facharbeit/Hashfunktion| Hashfunktion]], die auch Alice verwendet hat, anwenden. Die Information, welche [[Benutzer:Deininger_Matthias/Facharbeit/Hashfunktion| Hashfunktion]] von Alice verwendet wurde, ist in der Regel neben dem Hashwert in der Signatur enthalten. Anschließend kann Bob die Hashwerte vergleichen. Stimmen sie überein, wurde nichts verändert.<br> |
| − | Die [[Benutzer:Deininger_Matthias/Facharbeit/Hashfunktion| Hashfunktionen]] die unter der Bezeichnung SHA-2 (Secure Hash Algorithm) zusammengefasst werden und Hashwerte zwischen 224 und 512 Bit erzeugen, werden heutzutage häufig bei der digitalen Signatur eingesetzt. | + | Die [[Benutzer:Deininger_Matthias/Facharbeit/Hashfunktion| Hashfunktionen]], die unter der Bezeichnung SHA-2 (Secure Hash Algorithm) zusammengefasst werden und Hashwerte zwischen 224 und 512 Bit erzeugen, werden heutzutage häufig bei der digitalen Signatur eingesetzt.<br> |
| − | + | ||
| − | + | ||
| − | + | ||
<br> | <br> | ||
| + | <div style = "background-color: #BEFF9E; border: 2px solid #E5CC00;border-color: green;padding:5px;"> | ||
| + | <u>Aufgabe:</u><br> | ||
| + | Wie könnte es Alice mit den bereits kennen gelernten Methoden erreichen, dass Mallory auch den mitgesendeten Klartext nicht lesen kann?</div><br> | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
Zunächst sollte Alice die Nachricht signieren und anschließend sowohl Nachricht als auch Signatur mit dem öffentlichen Schlüssel von Bob verschlüsseln. Man spricht hier auch von einem kryptographischen Umschlag.<br> | Zunächst sollte Alice die Nachricht signieren und anschließend sowohl Nachricht als auch Signatur mit dem öffentlichen Schlüssel von Bob verschlüsseln. Man spricht hier auch von einem kryptographischen Umschlag.<br> | ||
| Zeile 45: | Zeile 45: | ||
© Klaus Schmeh aus "Kryptografie. Verfahren–Protokolle–Infrastrukturen" </div> | © Klaus Schmeh aus "Kryptografie. Verfahren–Protokolle–Infrastrukturen" </div> | ||
<br> | <br> | ||
| − | Um Problemen bei der Signierung vorzubeugen, sollten Alice und Bob zur Signatur ein gesondertes Schlüsselpaar generieren, so dass für Alice, wie auch | + | Um Problemen bei der Signierung vorzubeugen, sollten Alice und Bob zur Signatur ein gesondertes Schlüsselpaar generieren, so dass für den Schlüssel von Alice, wie auch den von Bob gilt:<br> |
<br> | <br> | ||
<math>n_{Signieren}< t\ und\ n_{Verschluesseln}\ge t\ ; t \in \N</math>, wobei t in Absprache zwischen Alice und Bob festgelegt wird.<br> | <math>n_{Signieren}< t\ und\ n_{Verschluesseln}\ge t\ ; t \in \N</math>, wobei t in Absprache zwischen Alice und Bob festgelegt wird.<br> | ||
<br> | <br> | ||
[[Bild:Anwendung2.gif|left|Anwendung des RSA-Algorithmus]] | [[Bild:Anwendung2.gif|left|Anwendung des RSA-Algorithmus]] | ||
| − | [http://garkbit.wor.net/rsa/ '''Signieren kannst du hier selbst ausprobieren. Viel Spaß!''']<br> | + | [http://garkbit.wor.net/rsa/sig.php '''Signieren kannst du hier selbst ausprobieren. Viel Spaß!''']<br> |
[[Bild:Homepage.PNG|300px]] | [[Bild:Homepage.PNG|300px]] | ||
<br> | <br> | ||
Die gerade vorgestellte digitale Signatur stellt eine zentrale Ergänzung zur RSA-Verschlüsselung dar, weil die digitale Signatur dazu beiträgt, die generellen Ziele der Kryptographie zu erfüllen.<br> | Die gerade vorgestellte digitale Signatur stellt eine zentrale Ergänzung zur RSA-Verschlüsselung dar, weil die digitale Signatur dazu beiträgt, die generellen Ziele der Kryptographie zu erfüllen.<br> | ||
Mit der digitalen Signatur lässt sich durch zusätzliche normale RSA-Verschlüsselung | Mit der digitalen Signatur lässt sich durch zusätzliche normale RSA-Verschlüsselung | ||
| − | Vertraulichkeit erreichen. Darüber hinaus ist in der Regel die von Alice und Bob gewünschte | + | '''Vertraulichkeit''' erreichen. Darüber hinaus ist in der Regel die von Alice und Bob gewünschte |
| − | Authentizität gewährleistet, wobei man hier einmal die Teilnehmerauthentizität (peer entity authentication) und die Nachrichtenauthentizität (message authentication ) unterscheiden kann. Ersteres garantiert, dass ein Teilnehmer eindeutig identifiziert werden kann und | + | '''Authentizität''' gewährleistet, wobei man hier einmal die Teilnehmerauthentizität (''peer entity authentication'') und die Nachrichtenauthentizität (''message authentication'') unterscheiden kann. Ersteres garantiert, dass ein Teilnehmer eindeutig identifiziert werden kann und das zweite Verfahren stellt sicher, dass der Ursprung einer Nachricht zweifelsfrei ermittelt werden kann. |
| − | Darüber hinaus können Dateien nicht unbemerkt verändert werden, was das Ziel der Integrität erfüllt. Zuletzt ist gegenüber einem unabhängigen Dritten auch eindeutig nachweisbar, dass eine Datei die | + | Darüber hinaus können Dateien nicht unbemerkt verändert werden, was das Ziel der '''Integrität''' erfüllt. Zuletzt ist gegenüber einem unabhängigen Dritten auch eindeutig nachweisbar, dass eine Datei die Bob von Alice erhalten hat, wirklich von Alice stammt, somit ist auch '''Verbindlichkeit''' gegeben.<ref>vgl. [1, S.2]</ref> <br> |
<br> | <br> | ||
Doch wer gewährleistet eigentlich, dass die Schlüsselpaare, die verwendet werden, auch wirklich den realen Personen gehören, für die sie sich ausgeben. Auf das Beispiel bezogen: Wer kann sicherstellen, dass Bob auch wirklich den öffentlichen Schlüssel von Alice erhalten hat und sich dahinter nicht Mallory verbirgt (vgl. [[Benutzer:Deininger_Matthias/Facharbeit/Angriffe_auf_RSA#Man-in-the-middle-Attacke| Man-in-the-middle-Attacke]])? Klaus Schmeh drückt es in seinem Buch „Kryptografie“ so aus; „Das Problem [...] ist, dass man einem öffentlichen Schlüssel nicht ansieht, wem er gehört“ <ref>[8, S.493]</ref>.<br> | Doch wer gewährleistet eigentlich, dass die Schlüsselpaare, die verwendet werden, auch wirklich den realen Personen gehören, für die sie sich ausgeben. Auf das Beispiel bezogen: Wer kann sicherstellen, dass Bob auch wirklich den öffentlichen Schlüssel von Alice erhalten hat und sich dahinter nicht Mallory verbirgt (vgl. [[Benutzer:Deininger_Matthias/Facharbeit/Angriffe_auf_RSA#Man-in-the-middle-Attacke| Man-in-the-middle-Attacke]])? Klaus Schmeh drückt es in seinem Buch „Kryptografie“ so aus; „Das Problem [...] ist, dass man einem öffentlichen Schlüssel nicht ansieht, wem er gehört“ <ref>[8, S.493]</ref>.<br> | ||
Aktuelle Version vom 23. Dezember 2010, 03:39 Uhr
RSA-Signaturverfahren
Mallory kann die Nachrichten von Alice an Bob abfangen. Er kann die verschlüsselten Nachrichten zwar nicht entschlüsseln, aber einfach Teile löschen und den gekürzten Text anschließend an Bob weitersenden. Wenn Bob die Chiffre entschlüsselt, wird er entweder ein Buchstabenpuzzle ohne jeglichen Sinn erhalten, wodurch Mallorys Manipulation enttarnt wäre. Gelingt es Mallory jedoch, ganze Wörter zu entfernen, so erscheint der Text sinnentstellt bei Bob und dieser erkennt unter Umständen gar nicht, dass Mallory am Werk war.
Um das zu verhindern, sollten Alice und Bob die Nachricht signieren, was einer Umkehrung der RSA-Verschlüsselung gleich kommt.
(1) Zur Signierung führt Alice die folgenden Schritte aus:
- (a) Alice berechnet die Signatur:
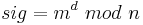
- (b) Alice übermittelt die Signatur sig an Bob.
(2) Zur Verifizierung und zum Erhalt der Nachricht führt Bob die folgenden Schritte aus:
- (a) Bob besorgt sich den authentischen öffentlichen Schlüssel (n, e) von Alice.
- (b) Bob berechnet
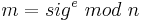 . Wenn
. Wenn 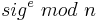 kein plausibler Klartext ist, wird die Signatur abgelehnt, andernfalls wird sie akzeptiert und
kein plausibler Klartext ist, wird die Signatur abgelehnt, andernfalls wird sie akzeptiert und 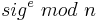 als m anerkannt.
als m anerkannt.
Wenn man das Signaturprotokoll so anwendet, wie es oben beschrieben ist, ergibt sich das Problem, dass die Signatur die gleiche Länge besitzt, wie das zu unterzeichnende Dokument, was auch bedeutet, dass ein ziemlich hoher Zeitbedarf zur Signierung nötig ist.
Der Vorteil bei dem Verfahren ist jedoch, dass sogenanntes „Message Recovery“ besteht. Dies bedeutet, dass die Originalnachricht bei der Verifizierung aus der Signatur wieder gewonnen werden kann.
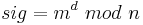
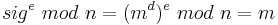
RSA wird gewöhnlich in Blöcken verschlüsselt, da für die Nachricht m gelten muss m < n. Mallory hat daher unter Umständen die Möglichkeit, einzelne Blöcke der Signatur zu entfernen, so dass sich beim Entschlüsseln dennoch ein sinnvoller, vermutlich aber sinnentstellter Text ergibt. Der Angriff ist also noch nicht abgewehrt.
Eine mögliche Lösung für das Problem besteht in der Verwendung von sog. Hashfunktionen H(m), mit deren Hilfe es möglich ist, Nachrichten nahezu beliebiger Länge auf eine durch die Hashfunktion festgelegte Größe zusammenzufassen. Dieses Zusammenfassen kann auch als „message digest“ bezeichnet werden.
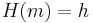
Anschließend sollte der gebildete Hashwert h, also die gehashte Nachricht mit oben beschriebenem Protokoll signiert werden, was dank der Kürze der kryptographischen Prüfsumme meist deutlich schneller möglich ist und überdies noch Speicherplatz spart. Dieses
Vorgehen kann man als Hash-and-Sign-Verfahren bezeichnen.
Wichtig ist hierbei zu erwähnen, dass es sich bei Hashfunktionen vermutlich um Einwegfunktionen handelt, die nicht effizient umkehrbar sind.
Folglich sollte Alice neben dem signierten Hashwert auch die ursprüngliche Nachricht (Urbild) an Bob senden.
Nach dem Erhalt der Nachricht von Alice, empfiehlt es sich für Bob, zunächst die Signatur von Alice zu verifizieren. Dazu kann Bob die Signatur mit Alices öffentlichem Schlüssel dechiffrieren, worauf er den Signaturhashwert erhält. Um zu überprüfen, ob die Originalnachricht oder die Signatur von Mallory verändert wurde, hat er die Möglichkeit, aus dem unverschlüsselten Klartext ebenfalls einen Hashwert zu bilden. Dazu sollte Bob, um ein verwertbares Ergebnis zu erhalten, die gleiche Hashfunktion, die auch Alice verwendet hat, anwenden. Die Information, welche Hashfunktion von Alice verwendet wurde, ist in der Regel neben dem Hashwert in der Signatur enthalten. Anschließend kann Bob die Hashwerte vergleichen. Stimmen sie überein, wurde nichts verändert.
Die Hashfunktionen, die unter der Bezeichnung SHA-2 (Secure Hash Algorithm) zusammengefasst werden und Hashwerte zwischen 224 und 512 Bit erzeugen, werden heutzutage häufig bei der digitalen Signatur eingesetzt.
Aufgabe:
Um Problemen bei der Signierung vorzubeugen, sollten Alice und Bob zur Signatur ein gesondertes Schlüsselpaar generieren, so dass für den Schlüssel von Alice, wie auch den von Bob gilt:
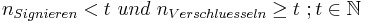 , wobei t in Absprache zwischen Alice und Bob festgelegt wird.
, wobei t in Absprache zwischen Alice und Bob festgelegt wird.
Signieren kannst du hier selbst ausprobieren. Viel Spaß!
Die gerade vorgestellte digitale Signatur stellt eine zentrale Ergänzung zur RSA-Verschlüsselung dar, weil die digitale Signatur dazu beiträgt, die generellen Ziele der Kryptographie zu erfüllen.
Mit der digitalen Signatur lässt sich durch zusätzliche normale RSA-Verschlüsselung
Vertraulichkeit erreichen. Darüber hinaus ist in der Regel die von Alice und Bob gewünschte
Authentizität gewährleistet, wobei man hier einmal die Teilnehmerauthentizität (peer entity authentication) und die Nachrichtenauthentizität (message authentication) unterscheiden kann. Ersteres garantiert, dass ein Teilnehmer eindeutig identifiziert werden kann und das zweite Verfahren stellt sicher, dass der Ursprung einer Nachricht zweifelsfrei ermittelt werden kann.
Darüber hinaus können Dateien nicht unbemerkt verändert werden, was das Ziel der Integrität erfüllt. Zuletzt ist gegenüber einem unabhängigen Dritten auch eindeutig nachweisbar, dass eine Datei die Bob von Alice erhalten hat, wirklich von Alice stammt, somit ist auch Verbindlichkeit gegeben.[3]
Doch wer gewährleistet eigentlich, dass die Schlüsselpaare, die verwendet werden, auch wirklich den realen Personen gehören, für die sie sich ausgeben. Auf das Beispiel bezogen: Wer kann sicherstellen, dass Bob auch wirklich den öffentlichen Schlüssel von Alice erhalten hat und sich dahinter nicht Mallory verbirgt (vgl. Man-in-the-middle-Attacke)? Klaus Schmeh drückt es in seinem Buch „Kryptografie“ so aus; „Das Problem [...] ist, dass man einem öffentlichen Schlüssel nicht ansieht, wem er gehört“ [4].
Die Frage, wie man dem öffentlichen Schlüssel dennoch ansehen kann, von wem er stammt, wird auf der nächsten Seite beantwortet.
![]() weiter zur PKI und den hybriden Verfahren
weiter zur PKI und den hybriden Verfahren
zurück zur Übersicht



