RSA-Algorithmus: Unterschied zwischen den Versionen
| (30 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <div style="text-align:right;">[[Bild:Buch.PNG]][[Benutzer:Deininger_Matthias/Facharbeit/Fachwortverzeichnis| Fachwortverzeichnis]]</div> | ||
===RSA-Algorithmus=== | ===RSA-Algorithmus=== | ||
<br> | <br> | ||
| Zeile 14: | Zeile 15: | ||
<tr> | <tr> | ||
<td>c (chiffre)</td> | <td>c (chiffre)</td> | ||
| − | <td> | + | <td>Chiffretext</td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
| Zeile 28: | Zeile 29: | ||
<br> | <br> | ||
Am 03.08. reist Bob mittags um 12 Uhr pünktlich mit dem Zug an. Alice hat ihre Recherchen bezüglich RSA erfolgreich abgeschlossen und erläutert Bob nun das RSA-Verfahren, das sie als geeignetes System ausgewählt hat.<br> | Am 03.08. reist Bob mittags um 12 Uhr pünktlich mit dem Zug an. Alice hat ihre Recherchen bezüglich RSA erfolgreich abgeschlossen und erläutert Bob nun das RSA-Verfahren, das sie als geeignetes System ausgewählt hat.<br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br> | <br> | ||
| Zeile 55: | Zeile 41: | ||
(1) Alice erzeugt zwei große Primzahlen p und q von ungefähr der gleichen Länge, wobei die Länge der einzelnen Primzahlen zwischen 512 und 2048 Bit betragen sollte.<br> | (1) Alice erzeugt zwei große Primzahlen p und q von ungefähr der gleichen Länge, wobei die Länge der einzelnen Primzahlen zwischen 512 und 2048 Bit betragen sollte.<br> | ||
(2) Alice berechnet <math>n = p\cdot q</math> und <math>\varphi(n)= (p-1)\cdot(q-1)</math>.<br> | (2) Alice berechnet <math>n = p\cdot q</math> und <math>\varphi(n)= (p-1)\cdot(q-1)</math>.<br> | ||
| − | (3) Alice wählt eine Zahl <math>e | + | (3) Alice wählt eine Zahl <math>e, so\ dass\ gilt\ 1 <e < < \varphi(n)</math>, mit <math>ggT(e, \varphi(n)) =1</math> [Begründung folgt später beim Beweis des RSA-Kryptosystems]<br> |
| − | (4) Alice berechnet <math>d = e^{-1}\ mod\ \varphi(n)</math><br> | + | (4) Alice berechnet <math>d = e^{-1}\ mod\ \varphi(n)</math><br> <math>\quad e\cdot d\equiv 1\ mod\ \{(p-1)\cdot (q-1)\}</math><br> |
| − | (5) Der öffentliche Schlüssel von Alice ist ( | + | (5) Der öffentliche Schlüssel von Alice ist (e, n), der private Schlüssel (d, n)<br></div></td> |
<td><div style = "text-align: left; padding:10px; width: 500px;height: 200px; border: 2px solid #E5CC00;border-color: orange;">'''Algorithmus 3.1 '''<ref name=W14 /><br> | <td><div style = "text-align: left; padding:10px; width: 500px;height: 200px; border: 2px solid #E5CC00;border-color: orange;">'''Algorithmus 3.1 '''<ref name=W14 /><br> | ||
Zusammenfassung: Bob chiffriert eine Nachricht m für Alice, die diese dechiffriert.<br> | Zusammenfassung: Bob chiffriert eine Nachricht m für Alice, die diese dechiffriert.<br> | ||
<br> | <br> | ||
(1) Zur Chiffrierung führt Bob die folgenden Schritte aus:<br> | (1) Zur Chiffrierung führt Bob die folgenden Schritte aus:<br> | ||
| − | :(a) Bob besorgt sich den authentischen öffentlichen Schlüssel ( | + | :(a) Bob besorgt sich den authentischen öffentlichen Schlüssel (e, n) von Alice.<br> |
:(b) Bob berechnet <math>c = m^e\ mod\ n</math> <br> | :(b) Bob berechnet <math>c = m^e\ mod\ n</math> <br> | ||
:(c) Bob übermittelt c an Alice.<br> | :(c) Bob übermittelt c an Alice.<br> | ||
(2) Zur Dechiffrierung führt Alice den folgenden Schritt aus:<br> | (2) Zur Dechiffrierung führt Alice den folgenden Schritt aus:<br> | ||
| − | : Mit ihrem privaten Schlüssel ( | + | : Mit ihrem privaten Schlüssel (d, n) berechnet sie <math>c^d\ mod\ n = m</math><br></div> |
</td> | </td> | ||
</tr> | </tr> | ||
| Zeile 73: | Zeile 59: | ||
Bob kann sich nicht vorstellen, dass beim Entschlüsseln wirklich der Klartext wieder erscheint. Alice zeigt Bob den zugehörigen Satz und macht einen mathematischen Beweis, um Bob von der Korrektheit des Verfahrens zu überzeugen.<br> | Bob kann sich nicht vorstellen, dass beim Entschlüsseln wirklich der Klartext wieder erscheint. Alice zeigt Bob den zugehörigen Satz und macht einen mathematischen Beweis, um Bob von der Korrektheit des Verfahrens zu überzeugen.<br> | ||
<br> | <br> | ||
| − | '''Satz 3.2'''<ref name=W14 /> Es sei <math>n = p\cdot q</math> mit Primzahlen p und q, wobei <math>p \neq q</math>. Weiter gelte <math>e,d \in \N</math> mit <math> e\cdot d\ mod\ \varphi(n) =1</math>, und es sei <math>m\in [0, n-1]</math> eine Nachricht. Dann folgt | + | <div style = "border: 2px solid red; padding:0.75em;"> |
| + | '''Satz 3.2'''<ref name=W14 /> Es sei <math>n = p\cdot q</math> mit Primzahlen p und q, wobei <math>p \neq q</math>. Weiter gelte <math>e,d \in \N</math> mit <math> e\cdot d\ mod\ \varphi(n) =1</math>, und es sei <math>m\in [0, n-1]</math> eine Nachricht. Dann folgt:<br> | ||
<br> | <br> | ||
| − | <math>(m^e\ mod\ n)^d\ mod\ n = m</math>.<br> | + | <math>(m^e\ mod\ n)^d\ mod\ n = m</math>.</div><br> |
| − | < | + | <popup name="Beweis"> |
| − | <u>Beweis:</u><ref>[3, S.6]</ref> <math>c\equiv m^e\ | + | <u>Beweis:</u><ref>[3, S.6]</ref> <math>c\equiv m^e\ mod\ n \Rightarrow c^d\ \equiv m^{ed}\ mod\ n</math><br> |
<br> | <br> | ||
Wenn ggT (m,p) = 1, so gilt:<br> | Wenn ggT (m,p) = 1, so gilt:<br> | ||
<br> | <br> | ||
| − | <math>m^{ed} = m^{k\cdot (p-1)\cdot (q-1)+1} = (m^{k\cdot (q-1) )(p-1)} \cdot m </math><br> | + | <math>m^{ed} = m^{k\cdot (p-1)\cdot (q-1)+1} = (m^{k\cdot (q-1) )(p-1)}) \cdot m </math><br> |
<br> | <br> | ||
| − | und daher nach dem Satz von Fermat <math>m^{ed} \equiv 1\cdot m \equiv m\ | + | und daher nach dem Satz von Fermat <math>m^{ed} \equiv 1\cdot m \equiv m\ mod\ p</math><br><br> |
| − | Ist m nicht zu p teilerfremd, so folgt <math>m^{ed} \equiv 0 \equiv m\ | + | Ist m nicht zu p teilerfremd, so folgt <math>m^{ed} \equiv 0 \equiv m\ mod\ p</math>. Analog ergibt sich <math>m^{ed} \equiv m\ mod\ q</math>.<br> |
Insgesamt folgt, dass sowohl p als auch q und damit auch ihr Produkt <math>p\cdot q= n</math> Teiler von | Insgesamt folgt, dass sowohl p als auch q und damit auch ihr Produkt <math>p\cdot q= n</math> Teiler von | ||
<math>m^{ed}-m\ </math> sind. Also gilt:<br> | <math>m^{ed}-m\ </math> sind. Also gilt:<br> | ||
| − | <br> <math>m^{ed} -m = k\cdot p\cdot q =k\cdot n\ oder\ (m^{ed} -m) \equiv 0\ | + | <br> <math>m^{ed} -m = k\cdot p\cdot q =k\cdot n\ oder\ (m^{ed} -m) \equiv 0\ mod\ \{p\cdot q\}</math><br> |
<br> | <br> | ||
| − | Damit gilt: <math>(m^{ed} -m) \equiv (m-m) \equiv 0\ | + | Damit gilt: <math>(m^{ed} -m) \equiv (m-m) \equiv 0\ mod\ \{p\cdot q\}</math><br> |
<br> | <br> | ||
| − | + | Daraus folgt: | |
<br> | <br> | ||
| − | <math>m^{ed} \equiv m\ | + | <math>m^{ed} \equiv m\ mod\ \{p\cdot q\}\ oder\ m^{ed} \equiv m\ mod\ n\ oder\ m^{ed}\ mod\ n = m</math> □<br> |
| + | <br> | ||
| + | </popup> | ||
<br> | <br> | ||
Nachdem sich Bob nach der „Modulo-Inverse“-Frage von Alice auch mit den mathematischen Grundlagen von RSA beschäftigt hat, erkennt er, dass Alice recht hat und bei der Dechiffrierung tatsächlich wieder der Klartext erscheint.<br> | Nachdem sich Bob nach der „Modulo-Inverse“-Frage von Alice auch mit den mathematischen Grundlagen von RSA beschäftigt hat, erkennt er, dass Alice recht hat und bei der Dechiffrierung tatsächlich wieder der Klartext erscheint.<br> | ||
| Zeile 113: | Zeile 102: | ||
für <math>\varphi(n)= (p-1)\cdot (q-1)= (5-1)\cdot (17-1)=4\cdot 16 =64</math><br> | für <math>\varphi(n)= (p-1)\cdot (q-1)= (5-1)\cdot (17-1)=4\cdot 16 =64</math><br> | ||
<br> | <br> | ||
| − | für e mit 0 < e << | + | für e mit 0 < e << 64 wählt er e = 5, so dass gilt ggT(5,64) = 1<br> |
<br> | <br> | ||
(5,85) ist damit der öffentliche Schlüssel von Bob, den er Alice übergibt, so dass sie damit die Nachricht an ihn verschlüsseln kann.<br> | (5,85) ist damit der öffentliche Schlüssel von Bob, den er Alice übergibt, so dass sie damit die Nachricht an ihn verschlüsseln kann.<br> | ||
<br> | <br> | ||
| − | Anschließend bestimmt Bob mittels des Algorithmus 2.1 die modulare Inverse d zu e mod n, die zusammen mit dem Modulus n seinen geheimen | + | Anschließend bestimmt Bob mittels des [[Benutzer:Deininger_Matthias/Facharbeit/Mathematische_Grundlagen_2| Algorithmus 2.1]] die modulare Inverse d zu e mod n, die zusammen mit dem Modulus n seinen geheimen privaten Schlüssel ergibt.<br> |
| − | <math>5\cdot d\ | + | <math>5\cdot d\ mod\ 64 = 1</math><br> |
<br> | <br> | ||
Berechnung des größten gemeinsamen Teilers mittels des Euklidischen Algorithmus, welcher zur Bestimmung der Vielfachsummendarstellung benötigt wird.<br> | Berechnung des größten gemeinsamen Teilers mittels des Euklidischen Algorithmus, welcher zur Bestimmung der Vielfachsummendarstellung benötigt wird.<br> | ||
| Zeile 125: | Zeile 114: | ||
<math>4\ = 1\cdot 4+0</math><br> | <math>4\ = 1\cdot 4+0</math><br> | ||
<br> | <br> | ||
| − | Hieraus | + | Hieraus bestimmt Bob die Vielfachsummendarstellung:<br> |
<math>1 = 5-1\cdot 4=</math><br> | <math>1 = 5-1\cdot 4=</math><br> | ||
<math>\quad = 5- 1\cdot (64-5\cdot 12)= 13\cdot 5-1\cdot 64</math><br> | <math>\quad = 5- 1\cdot (64-5\cdot 12)= 13\cdot 5-1\cdot 64</math><br> | ||
| Zeile 134: | Zeile 123: | ||
<br> | <br> | ||
Nun kann Alice die Nachricht m = 20 an Bob verschlüsseln<br> | Nun kann Alice die Nachricht m = 20 an Bob verschlüsseln<br> | ||
| − | <math>c= m^e\ | + | <math>c= m^e\ mod\ n</math><br> |
| − | <math>20^5\ | + | <math>20^5\ mod\ 85 = 3200000\ mod\ 85 = 5 = c</math><br> |
Anschließend übermittelt Alice die Chiffre c = 5 an Bob.<br> | Anschließend übermittelt Alice die Chiffre c = 5 an Bob.<br> | ||
<br> | <br> | ||
| Zeile 141: | Zeile 130: | ||
<br> | <br> | ||
Bob entschlüsselt die Nachricht mit seinem privaten Schlüssel, wie folgt:<br> | Bob entschlüsselt die Nachricht mit seinem privaten Schlüssel, wie folgt:<br> | ||
| − | <math>m= c^d\ | + | <math>m= c^d\ mod\ n</math><br> |
| − | <math>5^{13}\ | + | <math>5^{13}\ mod\ 85 = 1220703125\ mod\ 85 = 20 = m </math><br> |
<br> | <br> | ||
| − | Bevor du | + | Bevor du gemeinsam mit Alice und Bob zur praktischen Übung an einem Computerprogramm übergehen kannst, solltest du wissen, was sich hinter ASCII verbirgt.<br> |
<br> | <br> | ||
| − | Da man | + | Da man in der Regel Texte, also Ansammlungen von Buchstaben und Zahlen, verschlüsseln möchte, Programme aber nur Zahlen chiffrieren können, wurde bereits in den 1960er Jahren der [http://de.wikipedia.org/wiki/American_Standard_Code_for_Information_Interchange#ASCII-Tabelle ASCII]- Standard (American Standard Code for Information Interchange) von der ''American Standards Association'' entwickelt. Mit [http://de.wikipedia.org/wiki/American_Standard_Code_for_Information_Interchange#ASCII-Tabelle ASCII] ist es möglich, jede Ziffer und jeden Buchstaben als Zahl zu repräsentieren. Dieser [http://de.wikipedia.org/wiki/American_Standard_Code_for_Information_Interchange#ASCII-Tabelle ASCII-Code] kann anschließend verschlüsselt werden. Nach dem Dechiffrieren kann der [http://de.wikipedia.org/wiki/American_Standard_Code_for_Information_Interchange#ASCII-Tabelle ASCII-Code], wieder in die entsprechenden Buchstaben und Ziffern umgewandelt werden, so dass man den Klartext zurückerhält.<ref>vgl. [4, S. 394 f.]</ref><br> |
<br> | <br> | ||
<popup name="Für Interessierte: Die Gefahr des gleichen Modulus "> | <popup name="Für Interessierte: Die Gefahr des gleichen Modulus "> | ||
| − | Wenn zwei Benutzer den gleichen Modulus n besitzen, also auch gleiche Primzahlen p und q haben, könnten sie mithilfe des öffentlichen Schlüssels e des | + | Wenn zwei Benutzer den gleichen Modulus n besitzen, also auch gleiche Primzahlen p und q haben, könnten sie mithilfe des öffentlichen Schlüssels e des Anderen, dessen privaten Schlüssel d (= modulare Inverse zu e) berechnen und somit die verschlüsselten Nachrichten des anderen lesen. Es ist deshalb darauf zu achten, dass niemals zwei Personen den gleichen Modulus n besitzen, bei 200-stelligen Moduli, die in der Praxis eingesetzt werden, ist dies aber ohnehin unrealistisch. |
</popup> | </popup> | ||
<br><br> | <br><br> | ||
[[Bild:Anwendung2.gif|left|Anwendung des RSA-Algorithmus]] | [[Bild:Anwendung2.gif|left|Anwendung des RSA-Algorithmus]] | ||
| − | [http://garkbit.wor.net/rsa/ '''Hier kannst du das neu erworbene Wissen praktisch ausprobieren. Viel Spaß!'''] | + | [http://garkbit.wor.net/rsa/ '''Hier kannst du das neu erworbene Wissen praktisch ausprobieren. Viel Spaß!''']<br> |
| + | [[Bild:Homepage.PNG|400px]] | ||
<br> | <br> | ||
<br> | <br> | ||
Aktuelle Version vom 23. Dezember 2010, 02:53 Uhr
RSA-Algorithmus
Nachfolgende Abkürzungen benötigst du für den RSA-Algorithmus:
| Abkürzung | Bedeutung |
|---|---|
| m (message) | Klartext |
| c (chiffre) | Chiffretext |
| e (encryption) | Verschlüsselungsparameter |
| d (decryption) | Entschlüsselungsparameter |
Am 03.08. reist Bob mittags um 12 Uhr pünktlich mit dem Zug an. Alice hat ihre Recherchen bezüglich RSA erfolgreich abgeschlossen und erläutert Bob nun das RSA-Verfahren, das sie als geeignetes System ausgewählt hat.
| Public-Key-RSA-Schlüsselerzeugung: | Public-Key-RSA-Ver- und Entschlüsselung: |
|---|---|
Algorithmus 3.0[1] (1) Alice erzeugt zwei große Primzahlen p und q von ungefähr der gleichen Länge, wobei die Länge der einzelnen Primzahlen zwischen 512 und 2048 Bit betragen sollte. |
Algorithmus 3.1 [1]
Zusammenfassung: Bob chiffriert eine Nachricht m für Alice, die diese dechiffriert.
(2) Zur Dechiffrierung führt Alice den folgenden Schritt aus:
|
Bob kann sich nicht vorstellen, dass beim Entschlüsseln wirklich der Klartext wieder erscheint. Alice zeigt Bob den zugehörigen Satz und macht einen mathematischen Beweis, um Bob von der Korrektheit des Verfahrens zu überzeugen.
Satz 3.2[1] Es sei 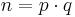 mit Primzahlen p und q, wobei
mit Primzahlen p und q, wobei 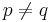 . Weiter gelte
. Weiter gelte 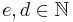 mit
mit 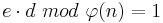 , und es sei
, und es sei ![m\in [0, n-1]](/images/math/7/0/7/7076a665adeb47067a38a1be448a3b03.png) eine Nachricht. Dann folgt:
eine Nachricht. Dann folgt:
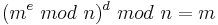 .
.
Nachdem sich Bob nach der „Modulo-Inverse“-Frage von Alice auch mit den mathematischen Grundlagen von RSA beschäftigt hat, erkennt er, dass Alice recht hat und bei der Dechiffrierung tatsächlich wieder der Klartext erscheint.
Wer einen ausführlicheren Beweis wünscht, der findet diesen hier.
Nachfolgend möchten Alice und Bob das Verfahren zum ersten Mal testen und wählen daher als Klartext die Zahl 20. Da sie noch kein Computerprogramm haben, mit dessen Hilfe sich das Verfahren auch mit großen Moduli n einfach umsetzen lässt, wählen sie zu Übungszwecken kleine Primzahlen p und q.
Schlüsselerzeugung:
Bob wählt:
p = 5
q = 17
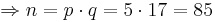
für 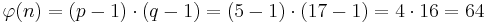
für e mit 0 < e << 64 wählt er e = 5, so dass gilt ggT(5,64) = 1
(5,85) ist damit der öffentliche Schlüssel von Bob, den er Alice übergibt, so dass sie damit die Nachricht an ihn verschlüsseln kann.
Anschließend bestimmt Bob mittels des Algorithmus 2.1 die modulare Inverse d zu e mod n, die zusammen mit dem Modulus n seinen geheimen privaten Schlüssel ergibt.
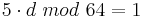
Berechnung des größten gemeinsamen Teilers mittels des Euklidischen Algorithmus, welcher zur Bestimmung der Vielfachsummendarstellung benötigt wird.
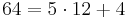
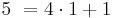
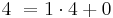
Hieraus bestimmt Bob die Vielfachsummendarstellung:
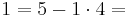
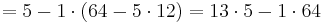
d= 13 => Der private Schlüssel von Bob lautet (13,85)
Verschlüsselung:
Nun kann Alice die Nachricht m = 20 an Bob verschlüsseln
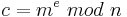
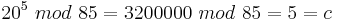
Anschließend übermittelt Alice die Chiffre c = 5 an Bob.
Entschlüsselung:
Bob entschlüsselt die Nachricht mit seinem privaten Schlüssel, wie folgt:
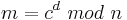
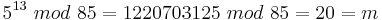
Bevor du gemeinsam mit Alice und Bob zur praktischen Übung an einem Computerprogramm übergehen kannst, solltest du wissen, was sich hinter ASCII verbirgt.
Da man in der Regel Texte, also Ansammlungen von Buchstaben und Zahlen, verschlüsseln möchte, Programme aber nur Zahlen chiffrieren können, wurde bereits in den 1960er Jahren der ASCII- Standard (American Standard Code for Information Interchange) von der American Standards Association entwickelt. Mit ASCII ist es möglich, jede Ziffer und jeden Buchstaben als Zahl zu repräsentieren. Dieser ASCII-Code kann anschließend verschlüsselt werden. Nach dem Dechiffrieren kann der ASCII-Code, wieder in die entsprechenden Buchstaben und Ziffern umgewandelt werden, so dass man den Klartext zurückerhält.[3]
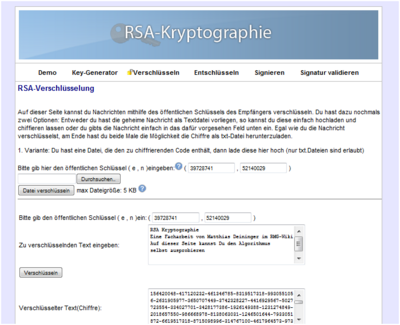
Hier kannst du das neu erworbene Wissen praktisch ausprobieren. Viel Spaß!
![]() weiter zur Sicherheit von RSA
weiter zur Sicherheit von RSA
zurück zur Übersicht
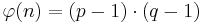 .
.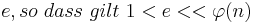 , mit
, mit 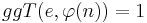 [Begründung folgt später beim Beweis des RSA-Kryptosystems]
[Begründung folgt später beim Beweis des RSA-Kryptosystems]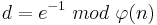
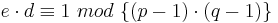
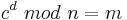
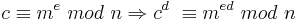
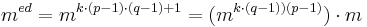
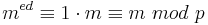
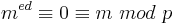 . Analog ergibt sich
. Analog ergibt sich 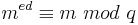 .
.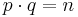 Teiler von
Teiler von
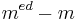 sind. Also gilt:
sind. Also gilt: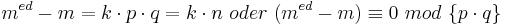
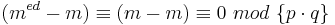
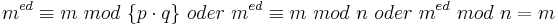 □
□


