Beweis 2: Unterschied zwischen den Versionen
| (5 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
Der Beweis basiert auf dem Satz von Euler und dem Satz von Fermat.<br> | Der Beweis basiert auf dem Satz von Euler und dem Satz von Fermat.<br> | ||
<br> | <br> | ||
| − | Danach gilt: <math>1\equiv m^{\varphi(n)}\ | + | Danach gilt: <math>1\equiv m^{\varphi(n)}\ mod\ n\ \mathrm{f{\ddot u}r}\ ggT(m,n)=1</math><br> |
| − | <math>und\ m^{p-1}\equiv 1\ | + | <math>und\ m^{p-1}\equiv 1\ mod\ p\ \mathrm{f{\ddot u}r}\ ggT(m,p) = 1\ und\ p \in \mathbb P (Primzahl)</math><br> |
<br> | <br> | ||
| − | 1. Mit <math>e\cdot d\equiv 1\ | + | 1. Mit <math>e\cdot d\equiv 1\ mod\ \varphi(n)</math>, d.h. <math>e\cdot d = k\cdot \varphi(n)+1</math> gilt:<br> |
| − | <math>m^{ed}\ | + | <math>m^{ed}\ mod\ n = m^{k\cdot \varphi(n)+1}\ mod\ n = m^{de}\ mod\ n</math>.<br> |
<br> | <br> | ||
| − | 2. Es bleibt also zu zeigen: <math>m^{ed}\ | + | 2. Es bleibt also zu zeigen: <math>m^{ed}\ mod\ n = m</math><br> |
Man unterscheidet nun die Fälle, dass p m teilt, und das p m nicht teilt. Falls p Teiler von m ist, gilt (mit einem passenden <math>i \in \N</math>)<br><br> | Man unterscheidet nun die Fälle, dass p m teilt, und das p m nicht teilt. Falls p Teiler von m ist, gilt (mit einem passenden <math>i \in \N</math>)<br><br> | ||
| − | <math>m^{ed}\ | + | <math>m^{ed}\ mod\ p = m^{k\cdot \varphi(n)+1}\ mod\ p</math><br> |
| − | + | <math>\quad = (i\cdot p)^{k\cdot \varphi(n)+1}\ mod\ p = 0 = m\ mod\ p</math><br> | |
| − | <math>\Rightarrow \quad i\cdot p \equiv 0\ | + | <math>\Rightarrow \quad i\cdot p \equiv 0\ mod\ p</math><br> |
<br> | <br> | ||
| − | Ist p nicht Teiler von m, dann gilt: ggT (p,m)= 1, da p eine Primzahl ist. <br> | + | Ist p nicht Teiler von m, dann gilt: ggT (p,m) = 1, da p eine Primzahl ist. <br> |
<br> | <br> | ||
Die Sätze von Euler und Fermat sind anwendbar und es gilt:<br> | Die Sätze von Euler und Fermat sind anwendbar und es gilt:<br> | ||
<br> | <br> | ||
| − | <math>m^{p-1} \equiv 1\ | + | <math>m^{p-1} \equiv 1\ mod\ p</math><br> |
<br> | <br> | ||
Da <math>(p-1)\quad \varphi(n)</math> teilt, gilt weiterhin:<br> | Da <math>(p-1)\quad \varphi(n)</math> teilt, gilt weiterhin:<br> | ||
<br> | <br> | ||
| − | <math>m^{k(p-1)\cdot (q-1)}\ | + | <math>m^{k(p-1)\cdot (q-1)}\ mod\ p = 1^{k(q-1)}\ mod\ p =1\ mod\ p</math><br> |
<br> | <br> | ||
| − | Also auch <math>m^{k(p-1)(q-1)+1}\ | + | Also auch <math>m^{k(p-1)(q-1)+1}\ mod\ p = 1\cdot m\ mod\ p</math><br> |
<br> | <br> | ||
| − | Und damit: <math>m^{k\cdot \varphi(n)+1}\ | + | Und damit: <math>m^{k\cdot \varphi(n)+1}\ mod\ p = m\ mod\ p</math><br> |
<br> | <br> | ||
| − | Also: <math>m^{ed}\ | + | Also: <math>m^{ed}\ mod\ p = m^{k\cdot \varphi(n)+1}\ mod\ p = m\ mod\ p</math><br> |
<br> | <br> | ||
| − | Analog gilt für <math>q: m^{ed}\ | + | Analog gilt für <math>q: m^{ed}\ mod\ q = m\ mod\ q</math><br> |
Es existiert weiterhin <math>i,j \in \N</math> mit<br> | Es existiert weiterhin <math>i,j \in \N</math> mit<br> | ||
<br> | <br> | ||
<math>i\cdot q +m = m^{ed} = j\cdot q +m\ und\ damit\ i\cdot p = j\cdot p</math><br> | <math>i\cdot q +m = m^{ed} = j\cdot q +m\ und\ damit\ i\cdot p = j\cdot p</math><br> | ||
<br> | <br> | ||
| − | da p und q Primzahlen sind, gilt es gibt | + | da p und q Primzahlen sind, gilt es gibt <math>\ r \in \N : j = r\cdot p,\ i = r\cdot q</math><br> |
<br> | <br> | ||
| − | Damit gilt: <math>m^{ed} = j\cdot q+m = r\cdot p\cdot q +m,\ also\ m^{ed}\ | + | Damit gilt: <math>m^{ed} = j\cdot q+m = r\cdot p\cdot q +m,\ also\ m^{ed}\ mod\ n = (r\cdot n + m)\ mod\ n = m</math><br> |
<br> | <br> | ||
Damit ist eindeutig gezeigt, dass sich die Nachricht m aus c wieder gewinnen lässt. □<br> | Damit ist eindeutig gezeigt, dass sich die Nachricht m aus c wieder gewinnen lässt. □<br> | ||
Aktuelle Version vom 23. Dezember 2010, 02:30 Uhr
Zu zeigen: 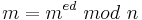
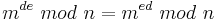
Der Beweis basiert auf dem Satz von Euler und dem Satz von Fermat.
Danach gilt: 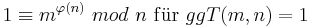
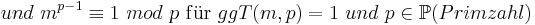
1. Mit 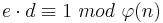 , d.h.
, d.h. 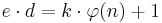 gilt:
gilt:
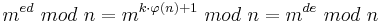 .
.
2. Es bleibt also zu zeigen: 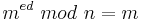
Man unterscheidet nun die Fälle, dass p m teilt, und das p m nicht teilt. Falls p Teiler von m ist, gilt (mit einem passenden 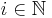 )
)
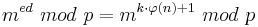
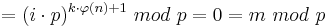
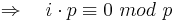
Ist p nicht Teiler von m, dann gilt: ggT (p,m) = 1, da p eine Primzahl ist.
Die Sätze von Euler und Fermat sind anwendbar und es gilt:
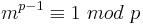
Da 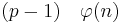 teilt, gilt weiterhin:
teilt, gilt weiterhin:
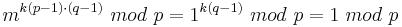
Also auch 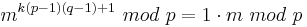
Und damit: 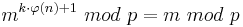
Also: 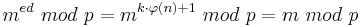
Analog gilt für 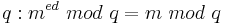
Es existiert weiterhin 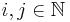 mit
mit
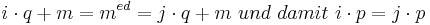
da p und q Primzahlen sind, gilt es gibt 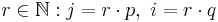
Damit gilt: 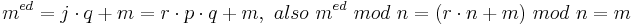
Damit ist eindeutig gezeigt, dass sich die Nachricht m aus c wieder gewinnen lässt. □
zurück zum RSA-Algorithmus
zurück zur Übersicht
Der auf dieser Seite dargestellte Beweis stammt aus [5, S.324 f.]
siehe dazu Literaturverzeichnis

