Quint-System5: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: ===Das pythagoreische Komma=== <br><br>Nach der 12. Quinte sollte man eigentlich wieder beim Anfangston angelangt sein. 12 Quinten sollten 7 Oktaven entsprechen.<br> J...)
 
(→‎Das pythagoreische Komma)
Zeile 8: Zeile 8:
  
 
Das pythagoreische Komma entspricht dem Verhältnis der 12 Quinten zu den 7 Oktaven<br><br>
 
Das pythagoreische Komma entspricht dem Verhältnis der 12 Quinten zu den 7 Oktaven<br><br>
−
<math>\frac {12 Q} {7 Ok} =  \frac {(\frac {3}{2})^{12}} {2^7} = 531441/524288 </math>
+
<math>\frac {12 Q} {7 Ok} =  \frac {(\frac {3}{2})^{12}} {2^7} = \frac {531441}{524288} </math>
−
Alternativ lässt sich das pythagoreische Komma auch durch die Differenz von Aptome und Leimma berechnen.
+
Alternativ lässt sich das pythagoreische Komma auch durch die Differenz von Aptome und Leimma berechnen.<br><br>
  
 
Leimma ist der oben berechnetet Halbtonschritt (Quarte-Ditonus) = <math>\textstyle \frac {256}{243}</math><br><br>
 
Leimma ist der oben berechnetet Halbtonschritt (Quarte-Ditonus) = <math>\textstyle \frac {256}{243}</math><br><br>
Zeile 19: Zeile 19:
 
Da die pythagoreische Tonleiter nur 6 Töne hat berechnet sich die Höhe des 6. Tons wie folgt:<br><br>  <math>H (A_6) = (\frac{9}{8})^6 = 2,02728653;</math><br><br>
 
Da die pythagoreische Tonleiter nur 6 Töne hat berechnet sich die Höhe des 6. Tons wie folgt:<br><br>  <math>H (A_6) = (\frac{9}{8})^6 = 2,02728653;</math><br><br>
 
Da wir uns nun etwas mehr als eine Oktave über unserem Ausgangston befinden, müssen wir diese wieder abziehen um die Abweichen vom Grundton festzustellen.
 
Da wir uns nun etwas mehr als eine Oktave über unserem Ausgangston befinden, müssen wir diese wieder abziehen um die Abweichen vom Grundton festzustellen.
−
2,02728653  - Ok = 2,02728653/2 = 1,013643265 ↔ 531441/524288
+
2,02728653  - Ok = 2,02728653/2 = 1,013643265 <math>\leftrightarrow \textstyle \frac{531441}{524288};</math><br>
 
In der pythagoreischen Tonleiter befinden sich 2 Halbtonschritte. Zusammen sind sie etwas kleiner ein Ganzton, genauer gesagt wenn man von einem Ganzton zwei Halbtonschritte abzieht erhält man das pythagoreische Komma, d.h. <math> \frac {\frac {9}{8}} {\frac {256}{243}^2}</math> = pythagoreisches Komma.
 
In der pythagoreischen Tonleiter befinden sich 2 Halbtonschritte. Zusammen sind sie etwas kleiner ein Ganzton, genauer gesagt wenn man von einem Ganzton zwei Halbtonschritte abzieht erhält man das pythagoreische Komma, d.h. <math> \frac {\frac {9}{8}} {\frac {256}{243}^2}</math> = pythagoreisches Komma.
 
Durch eine einfach Umformung lässt sich also die Behauptung A – L bestätigen:
 
Durch eine einfach Umformung lässt sich also die Behauptung A – L bestätigen:

Version vom 20. Dezember 2010, 10:13 Uhr

Das pythagoreische Komma



Nach der 12. Quinte sollte man eigentlich wieder beim Anfangston angelangt sein. 12 Quinten sollten 7 Oktaven entsprechen.
Jedoch gilt für 12 Quinten:

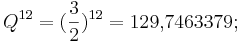
Q^{12} = (\frac{3}{2})^{12} = 129{,}7463379;

für 7 Oktaven gilt:

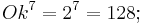
Ok^7 = 2^7 = 128;

Man sieht, dass die 12 Quinten die 7 Oktaven übertreffen.

Das pythagoreische Komma entspricht dem Verhältnis der 12 Quinten zu den 7 Oktaven

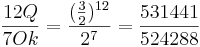\frac {12 Q} {7 Ok} = \frac {(\frac {3}{2})^{12}} {2^7} = \frac {531441}{524288} Alternativ lässt sich das pythagoreische Komma auch durch die Differenz von Aptome und Leimma berechnen.

Leimma ist der oben berechnetet Halbtonschritt (Quarte-Ditonus) = 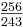\textstyle \frac {256}{243}

Aptome berechnet sich aus tonus – Leimma (Ganzton-Halbton) = 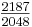\textstyle \frac {2187}{2048}

Das Verhältnis der 12 Quinten zu den 7 Oktaven entspricht der Differenz aus Aptome und Leimma, also

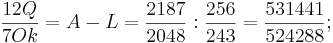
\frac{12Q}{7Ok}= A - L = \frac{2187}{2048} : \frac{256}{243} = \frac{531441}{524288};

Die Differenz aus Aptome und Leimma kann man aus folgender Gegebenheit ableiten:
der letzte Ton der pythagoreischen Tonleiter ist etwas höher als die Oktave. Wir haben oben folgende Formel für die pythagoreische Tonleiter definiert:

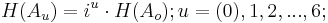
H(A_u) = i^u \cdot H(A_o); u = (0),1,2,...,6;

Da die pythagoreische Tonleiter nur 6 Töne hat berechnet sich die Höhe des 6. Tons wie folgt:

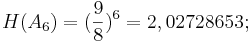
H (A_6) = (\frac{9}{8})^6 = 2,02728653;

Da wir uns nun etwas mehr als eine Oktave über unserem Ausgangston befinden, müssen wir diese wieder abziehen um die Abweichen vom Grundton festzustellen. 2,02728653 - Ok = 2,02728653/2 = 1,013643265 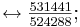\leftrightarrow \textstyle \frac{531441}{524288};
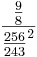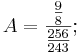
In der pythagoreischen Tonleiter befinden sich 2 Halbtonschritte. Zusammen sind sie etwas kleiner ein Ganzton, genauer gesagt wenn man von einem Ganzton zwei Halbtonschritte abzieht erhält man das pythagoreische Komma, d.h. \frac {\frac {9}{8}} {\frac {256}{243}^2} = pythagoreisches Komma. 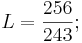Durch eine einfach Umformung lässt sich also die Behauptung A – L bestätigen: A = \frac {\frac {9}{8}} {\frac {256}{243}}; L = \frac {256}{243}; Für A – L gilt also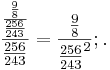 \frac {\frac {\frac {9}{8}} {\frac {256}{243}}}{\frac {256}{243}} = \frac {\frac {9}{8}} {\frac {256}{243}^2}; .

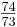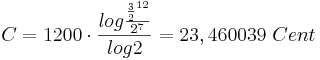Anmerkung: In der Literatur wird für das pythagoreische Komma oft auch der Wert \textstyle \frac{74}{73} angegeben. Allerdings ist dieser Wert eine Näherung. Umgerechnet in Cent beträgt das pythagoreische Komma: C = 1200 \cdot \frac {log\frac {\frac {3}{2}^{12}}{2^7}} {log 2} = 23,460039 \ Cent.

weiter zum pythagoreischen Quintenzirkel und der pythagoreischen C-Dur Tonleiter

zurück zur Übersichtsseite

Von „http://rmg.zum.de/index.php?title=Benutzer:Grieninger_Sebastian/Facharbeit/Quint-System5&oldid=39346“