Wiederholung des Grundwertes: Unterschied zwischen den Versionen
(→Wiederholung zu Berechnung des Grundwertes) |
(→Wiederholung zu Berechnung des Grundwertes) |
||
| Zeile 58: | Zeile 58: | ||
Grundwert = <math>\frac{5Euro}{0,2}</math> = 25 Euro | Grundwert = <math>\frac{5Euro}{0,2}</math> = 25 Euro | ||
</div> | </div> | ||
| − | |||
<br /> | <br /> | ||
Version vom 11. Dezember 2010, 20:35 Uhr
Inhaltsverzeichnis |
Wiederholung zu Berechnung des Grundwertes
Wichtig!
- Der Grundwert wird auch als Bezugsgröße bezeichnet. Er steht für das „Ganze“. Prozentangaben beziehen sich also immer auf den Grundwert!
- Zur Berechnung des Grundwertes verwendet man, abgesehen vom Dreisatz, immer diese Fromel: Grundwert =
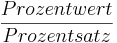
Bei der Berechnung des Grundwertes unterscheidet man drei Fälle:
Fall 1
Ein T-Shirt wird ist 20% reduziert. Dadurch spart man 5 €.
- Wie viel hat es vorher gekostet?
Gesucht ist hier der Wert, der 100% entspricht, wenn 20% 5€ entsprechen.
Lösung:
Diese Rechnung lässt sich auf 2 Weisen lösen.
- Dreisatz
20% des Grundwerts sind 5 €, das heißt
10% des Grundwerts sind 2,50 €, also sind
100% des Grundwerts 25 €
oder:
- Berechnung mit der allgemeinen Formel:
Grundwert =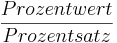
Bestimmung der angegebenen Größen:
Prozentwert sind die 5€ die das T-Shirt günstiger ist.
Prozentsatz sind hier die 20%
Allerdings rechnet man in der Regel mit der Dezimalzahl, die man durch die Division mit 100 erhält.
Man rechnet also mit 0,2 anstatt 20%
Daraus ergibt sich dann, durch Einsetzen in die Gleichung, folgende Rechnung:
Grundwert =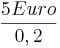 
= 25 Euro
Fall 2
Ein T-Shirt ist um 20% reduziert. Es kostet jetzt nur noch 20€.
- Wie viel hat es vorher gekostet?
Wieder sucht man den Wert, der 100%, also dem vorherigen Preis, entspricht.
Auch in diesem Fall rechnet man mit der Formel: Grundwert =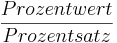
Prozentwert sind hier die 20€, die das T-Shirt jetzt kostet.
Auch hier benötigt man für die Bestimmung des Prozentsatzes eine Zwischenüberlegung:
Der Prozentwert = Grundwert - (Grundwert • 20%)
Hier subtrahiert man die beiden Werte, da der Preis reduziert wurde.
Setzt man auch hier für den Grundwert 100% ein so erhält man folgende Gleichung:
Prozentwert = 100% - (100% •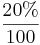 
) = 100% - 20% = 80%
--> Dadurch weiß man, dass der Prozentwert 80% des Grundwerts entspricht.
--> Der Prozentsatz ist hier also 80% (Auch hier dividiert man zur Rechnung durch 100)
Setzt man jetzt diese Werte in die Fromel ein so erhält man folgende Rechnung:
Grundwert =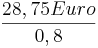 
= 25 Euro
Fall 3
Der Preis eines T-Shirts wird, bei einer Auktion, 15% teurer verkauft. Es kostet jetzt 28,75€.
- Wie hoch ist der normale Preis?
Auch hier ist der Wert gesucht, der 100%, also dem vorherigen Preis des T-Shirts, entspricht.
Diese Rechnung könnte man auch durch den Dreisatz lösen, allerdings bieten sich für die Berechnung mit dem Dreisatz eher ganze Zahlen an.
Daher nimmt man zur Berechnung dieses Grundwertes wieder die bekannte Formel:
Grundwert =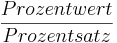
Man beginnt wieder mit der Bestimmung der Größen:
Prozentwert ist hier der Preis, für den das T-Shirt verkauft wurde, also 28,75€
Um den Prozentsatz zu berechnen muss man sich folgendes klarmachen:
Der Prozentwert = Grundwert + (Grundwert • 15%)
Setzt man nun für den Grundwert 100% ein, so erhält man folgende Gleichung:
Prozentwert = 100% + (100% •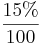 
) = 100% + 15% = 115%
Man addiert die beiden Werte, da der Preis erhöht wurde.
--> Dadurch weiß man nun, dass der Prozentwert 115% des Grundwertes entsrpicht.
--> Der Prozentsatz ist also 115% (Zur vereinfachten Rechnung dividiert man durch 100)
Setzen man nun die Werte in die Formel ein, erhält man folgende Rechnung:
Grundwert =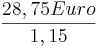 
= 25 Euro
