Angriffe auf RSA: Unterschied zwischen den Versionen
| Zeile 4: | Zeile 4: | ||
<br> | <br> | ||
====Brute–Force-Attacke==== | ====Brute–Force-Attacke==== | ||
| − | Zunächst betrachten wir die sogenannte Brute–Force-Attacke, also die vollständige Schlüsselsuche. Mallory probiert bei diesem Angriff alle möglichen privaten Schlüssel der Reihe nach durch. Bereits bei einer Schlüssellänge von 256 Bit für d ist es ein aussichtloses Verfahren, denn Mallory müsste im Durchschnitt <math>2^{255}</math> Schlüssel ausprobieren. Das entspricht <math>10^{76}</math> Schlüsseln - eine Zahl, die größer als die Anzahl der Atome in unserer Galaxie ist. (Anzahl der Atome in unserer Galaxie: <math>10^{67}</math>)<ref>vgl. [ | + | Zunächst betrachten wir die sogenannte Brute–Force-Attacke, also die vollständige Schlüsselsuche. Mallory probiert bei diesem Angriff alle möglichen privaten Schlüssel der Reihe nach durch. Bereits bei einer Schlüssellänge von 256 Bit für d ist es ein aussichtloses Verfahren, denn Mallory müsste im Durchschnitt <math>2^{255}</math> Schlüssel ausprobieren. Das entspricht <math>10^{76}</math> Schlüsseln - eine Zahl, die größer als die Anzahl der Atome in unserer Galaxie ist. (Anzahl der Atome in unserer Galaxie: <math>10^{67}</math>)<ref>vgl. [8, S.177]</ref> Allgemein bedeutet dies, dass man bei einer n-Bit Schlüssellänge mittels Brute-Force-Angriff <math>2^{n-1}</math> mögliche Schlüssel überprüfen muss, um die richtige Lösung zu erhalten. 2 bildet hierbei die Basis, da ein Bit lediglich die Werte 0 oder 1 annehmen kann.<br> |
| − | Betrachtet man die zugehörige [[Benutzer:Deininger_Matthias/Facharbeit/Mathematische_Grundlagen| Berechnungskomplexität]], so ergibt sich: O(<math>2^n</math>), also eine exponentielle Berechnungskomplexität. Definitionsgemäß gilt eine Brute-Force-Attacke damit als uneffizient.<ref>[ | + | Betrachtet man die zugehörige [[Benutzer:Deininger_Matthias/Facharbeit/Mathematische_Grundlagen| Berechnungskomplexität]], so ergibt sich: O(<math>2^n</math>), also eine exponentielle Berechnungskomplexität. Definitionsgemäß gilt eine Brute-Force-Attacke damit als uneffizient.<ref>[9, S.278]</ref><br> |
<br> | <br> | ||
====Man-in-the-middle-Attacke==== | ====Man-in-the-middle-Attacke==== | ||
Version vom 21. September 2010, 21:55 Uhr
Inhaltsverzeichnis |
Angriffe auf RSA
Prinzipiell unterscheidet man aktive und passive Angriffe, je nachdem ob Mallory aktiv in die Kommunikation eingreift oder lediglich die Kommunikation zwischen Alice und Bob mitliest und selbst nichts verändert.
Brute–Force-Attacke
Zunächst betrachten wir die sogenannte Brute–Force-Attacke, also die vollständige Schlüsselsuche. Mallory probiert bei diesem Angriff alle möglichen privaten Schlüssel der Reihe nach durch. Bereits bei einer Schlüssellänge von 256 Bit für d ist es ein aussichtloses Verfahren, denn Mallory müsste im Durchschnitt 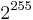 Schlüssel ausprobieren. Das entspricht
Schlüssel ausprobieren. Das entspricht 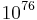 Schlüsseln - eine Zahl, die größer als die Anzahl der Atome in unserer Galaxie ist. (Anzahl der Atome in unserer Galaxie:
Schlüsseln - eine Zahl, die größer als die Anzahl der Atome in unserer Galaxie ist. (Anzahl der Atome in unserer Galaxie: 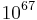 )[1] Allgemein bedeutet dies, dass man bei einer n-Bit Schlüssellänge mittels Brute-Force-Angriff
)[1] Allgemein bedeutet dies, dass man bei einer n-Bit Schlüssellänge mittels Brute-Force-Angriff 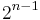 mögliche Schlüssel überprüfen muss, um die richtige Lösung zu erhalten. 2 bildet hierbei die Basis, da ein Bit lediglich die Werte 0 oder 1 annehmen kann.
mögliche Schlüssel überprüfen muss, um die richtige Lösung zu erhalten. 2 bildet hierbei die Basis, da ein Bit lediglich die Werte 0 oder 1 annehmen kann.
Betrachtet man die zugehörige Berechnungskomplexität, so ergibt sich: O(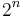 ), also eine exponentielle Berechnungskomplexität. Definitionsgemäß gilt eine Brute-Force-Attacke damit als uneffizient.[2]
), also eine exponentielle Berechnungskomplexität. Definitionsgemäß gilt eine Brute-Force-Attacke damit als uneffizient.[2]
Man-in-the-middle-Attacke
Ein weiterer Angriff, den Mallory ausführen kann, ist die Man-in-the-middle-Attacke, dieser Angriff ist gegen alle Public-Key-Verfahren wirksam.
Die Man-in-the-middle-Attacke, ein aktiver Angriff, beruht darauf, dass Mallory die Übermittlung der Daten zwischen Alice und Bob aktiv manipulieren kann. Er kann also auch die Nachrichten von Alice abfangen und statt dieser seine Nachrichten an Bob weitersenden.
Wenn Mallory dabei wie folgt vorgeht, wird er nicht einmal entdeckt.
Mallory gibt sich gegenüber Alice als Bob aus und sendet ihr seinen öffentlichen Schlüssel alias Bobs Schlüssel zu, so dass sie Mallorys öffentlichen Schlüssel zur Verschlüsselung der für Bob bestimmten Nachrichten verwendet. Im umgekehrten Fall gibt sich Mallory auch gegenüber Bob als Alice aus und sendet auch hier seinen öffentlichen Schlüssel an Bob. Wenn Mallory klug ist, entschlüsselt er die Nachricht, die beispielsweise von Alice stammt, mit seinem privaten Schlüssel, kann den Inhalt lesen, verschlüsselt die Nachricht anschließend wieder mit Bobs öffentlichem Schlüssel und sendet ihm die Nachricht von Alice zu. Dieser kann die Chiffre mit seinem privaten Schlüssel wieder dechiffrieren und erhält den von Alice versandten Text, ohne zu bemerken, dass dieser vorher bereits von Mallory gelesen wurde. Umgekehrtes funktioniert natürlich auch, wenn Bob eine Nachricht an Alice senden möchte.
Wie sich Alice und Bob von Anfang an gegen eine potentielle Man-in-the-middle-Attacke schützen können, erfährst du im Kapitel PKI.
Public-Key-Only-Attacke
Als Public-Key-only-Attacke wird die Tatsache beschrieben, dass sich Mallory mithilfe des öffentlichen Schlüssels beliebig viele Klartexte chiffrieren kann.
Unter Verwendung dieser Attacke lässt sich RSA leicht angreifen, weil es deterministisch ist, was bedeutet, dass man bei Verschlüsselung des gleichen Klartextes immer die gleiche Chiffre erhält.
Liegt Mallory ein abgefangener Chiffretext vor, dessen Inhalt er entschlüsseln möchte, so kann er sich eine Datenbank an verschlüsselten Wörtern und Sätzen mit entsprechender Entschlüsselung anlegen, mithilfe derer er die Chiffre brechen kann. Dazu vergleicht Mallory einfach die, in der Datenbank gespeicherten, verschlüsselten Daten mit der vorliegenden Chiffre und ersetzt bei jedem Treffer die Chiffrepassage durch den Klartext aus der Datenbank. In der Realität ist der Angriff, wie er gerade beschrieben wurde, eher unrealistisch, da zu viel Speicherplatz nötig wäre, um eine solche Datenbank zu erschaffen, doch prinzipiell lässt sich das RSA-Verfahren damit „brechen“.
Um sich vor diesem und ähnlichen, in der Realität eingesetzten, Angriff effektiv zu schützen, kann sogenanntes Padding eingesetzt werden.
Das Grundprinzip beruht darauf, dass in den Klartext Zufallsbits eingestreut werden, die bei der Verschlüsselung dafür sorgen, dass kein Chiffrat dem anderen gleicht, sogar wenn der identische Plaintext mehrmals verschlüsselt wird. Die Position der Zufallsbits im Text kann mittels eines Pseudozufallsgenerators (engl. Pseudo Random Number Generator = PRNG) bestimmt werden, so dass sich das Padding bei der Entschlüsselung leicht wieder rückgängig machen lässt und der Klartext unverändert aus der Padding-Chiffre hervorgeht. Ein bedeutendes Padding-Protokoll ist das, im Jahre 1995 entwickelte, OAEP-Verfahren (= Optimal Asymmetric Encryption Padding).
Wird Padding beim RSA-Algorithmus eingesetzt, kann die Verschlüsselung als semantisch sicher bezeichnet werden und sollte somit den oben beschriebenen Angriff vereiteln.
Ein selten wirksamer Angriff resultiert aus den Homomorphieeigenschaften des RSA-Verfahrens.
Bei den vorgestellten Angriffen handelt es sich selbstverständlich nur um eine Auswahl, es gibt noch zahlreiche weitere Attacken. Doch sobald man den Angriff kennt, kann man Abwehrstrategien entwerfen. Dank des großen Forschungsinteresses auf diesem Gebiet werden immer neue potentielle Angriffe von den Kryptoanalytikern entdeckt und entsprechende Gegenmaßnahmen gesucht.
Alice und Bob können ihre Nachricht nun zwar relativ sicher ver- und wieder entschlüsseln, doch das ist noch nicht genug, denn Mallory ist nicht untätig gewesen und hat sich einen anderen Angriff überlegt, der auf dem Übertragungsweg zwischen Alice und Bob ansetzt. Nachdem er aus der letzten unverschlüsselten Mail von Alice erfahren hat, dass sie RSA zur Verschlüsselung einsetzen möchte.
=> Diesen Angriff gilt es abzuwehren!
zurück zur Übersicht

