RSA-Signaturverfahren: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: Mallory kann die Nachrichten von Alice an Bob abfangen. Er kann die verschlüsselten Nachrichten zwar nicht entschlüsseln, aber einfach Teile löschen und den gekürzt...) |
|||
| Zeile 11: | Zeile 11: | ||
:(b) Bob berechnet <math>m = sig^e\ mod\ n</math>. Wenn <math>sig^e\ mod\ n</math> kein plausibler Klartext ist, wird die Signatur abgelehnt, andernfalls wird sie akzeptiert und <math>sig^e\ mod\ n</math> als m anerkannt.<br> | :(b) Bob berechnet <math>m = sig^e\ mod\ n</math>. Wenn <math>sig^e\ mod\ n</math> kein plausibler Klartext ist, wird die Signatur abgelehnt, andernfalls wird sie akzeptiert und <math>sig^e\ mod\ n</math> als m anerkannt.<br> | ||
(3) In einem Streitfall zwischen Alice und Bob kann ein neutraler Richter überprüfen, ob <math>sig^e\ mod\ n = m</math> gilt.<br> | (3) In einem Streitfall zwischen Alice und Bob kann ein neutraler Richter überprüfen, ob <math>sig^e\ mod\ n = m</math> gilt.<br> | ||
| + | <br> | ||
| + | Wenn man das Signaturprotokoll so anwendet, wie es oben beschrieben ist, ergibt sich das Problem, dass die Signatur die gleiche Länge besitzt, wie das zu unterzeichnende Dokument, was auch bedeutet, dass ein ziemlich hoher Zeitbedarf zur Signierung nötig ist. | ||
| + | Der Vorteil bei dem Verfahren ist jedoch, dass sogenanntes „Message Recovery“ besteht. Dies bedeutet, dass die Originalnachricht bei der Verifizierung aus der Signatur wieder gewonnen werden kann.<br> | ||
| + | <br> | ||
| + | <math>sig = m^d\ mod\ n </math><br> | ||
| + | <math> sig^e\ mod\ n = (m^d)^e\ mod\ n = m</math><br> | ||
| + | <br> | ||
| + | RSA wird gewöhnlich in Blöcken verschlüsselt, da für die Nachricht m gelten muss m < n. Mallory hat daher unter Umständen die Möglichkeit, einzelne Blöcke der Signatur zu entfernen, so dass sich beim Entschlüsseln dennoch ein sinnvoller, vermutlich aber sinnentstellter Text ergibt. Der Angriff ist also noch nicht abgewehrt.<br> | ||
| + | <br> | ||
| + | Eine mögliche Lösung für das Problem besteht in der Verwendung von sog. [[Benutzer:Deininger_Matthias/Facharbeit/Hashfunktion| Hashfunktion]], mit deren Hilfe es möglich ist, Nachrichten nahezu beliebiger Länge auf eine durch die [[Benutzer:Deininger_Matthias/Facharbeit/Hashfunktion| Hashfunktion]] festgelegte Größe zusammenzufassen. Dieses Zusammenfassen kann auch als „message digest“ bezeichnet werden.<br> | ||
| + | <math>H(m) = h\ </math><br> | ||
| + | Anschließend sollte der gebildete Hashwert, also die gehashte Nachricht mit oben beschriebenem Protokoll signiert werden, was dank der Kürze der kryptographischen Prüfsumme meist deutlich schneller möglich ist und überdies noch Speicherplatz spart. Dieses | ||
| + | Vorgehen kann man als Hash-and-Sign-Verfahren bezeichnen.<br> | ||
| + | <br> | ||
| + | Wichtig ist hierbei zu erwähnen, dass es sich bei [[Benutzer:Deininger_Matthias/Facharbeit/Hashfunktion| Hashfunktion]] vermutlich um Einwegfunktionen handelt, die nicht effizient umkehrbar sind. <br> | ||
| + | <br> | ||
| + | Folglich sollte Alice neben dem signierten Hashwert auch die ursprüngliche Nachricht (Urbild) an Bob senden. <br> | ||
| + | <br> | ||
| + | Nach dem Erhalt der Nachricht von Alice empfiehlt es sich für Bob zunächst die Signatur von Alice zu verifizieren. Dazu kann Bob die Signatur mit Alices öffentlichem Schlüssel dechiffrieren, worauf er den Signaturhashwert erhält. Um zu überprüfen, ob die Originalnachricht oder die Signatur von Mallory verändert wurde, hat er die Möglichkeit, aus dem unverschlüsselten Klartext ebenfalls einen Hashwert zu bilden. Dazu sollte Bob, um ein verwertbares Ergebnis zu erhalten, die gleiche [[Benutzer:Deininger_Matthias/Facharbeit/Hashfunktion| Hashfunktion]], die auch Alice verwendet hat, anwenden. Die Information, welche [[Benutzer:Deininger_Matthias/Facharbeit/Hashfunktion| Hashfunktion]] von Alice verwendet wurde, ist in der Regel neben dem Hashwert in der Signatur enthalten. Anschließend kann Bob die Hashwerte vergleichen. Stimmen sie überein, wurde nichts verändert.<br> | ||
| + | Die [[Benutzer:Deininger_Matthias/Facharbeit/Hashfunktion| Hashfunktion]] SHA-1 (Secure Hash Algorithm), die einen Hashwert von 160 Bit erzeugt, wird heutzutage häufig bei der digitalen Signatur eingesetzt.<br> | ||
| + | <br> | ||
Version vom 12. September 2010, 12:52 Uhr
Mallory kann die Nachrichten von Alice an Bob abfangen. Er kann die verschlüsselten Nachrichten zwar nicht entschlüsseln, aber einfach Teile löschen und den gekürzten Text anschließend an Bob weitersenden. Wenn Bob die Chiffre entschlüsselt, wird er entweder ein Buchstabenpuzzle ohne jeglichen Sinn erhalten, wodurch Mallorys Manipulation enttarnt wäre. Gelingt es Mallory jedoch, ganze Wörter zu entfernen, so erscheint der Text sinnentstellt bei Bob und dieser erkennt unter Umständen gar nicht, dass Mallory am Werk war.
Um das zu verhindern sollten Alice und Bob die Nachricht signieren, was einer Umkehrung der RSA-Verschlüsselung gleich kommt.
Algorithmus 4.0 (RSA-Public-Key-Signaturverfahren)
(1) Zur Signierung führt Alice die folgenden Schritte aus:
- (a) Alice berechnet die Signatur:
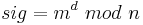
- (b) Alice übermittelt die Signatur sig an Bob.
(2) Zur Verifizierung und zum Erhalt der Nachricht führt Bob die folgenden Schritte aus:
- (a) Bob besorgt sich den authentischen öffentlichen Schlüssel (n, e) von Alice.
- (b) Bob berechnet
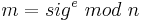 . Wenn
. Wenn 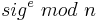 kein plausibler Klartext ist, wird die Signatur abgelehnt, andernfalls wird sie akzeptiert und
kein plausibler Klartext ist, wird die Signatur abgelehnt, andernfalls wird sie akzeptiert und 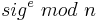 als m anerkannt.
als m anerkannt.
(3) In einem Streitfall zwischen Alice und Bob kann ein neutraler Richter überprüfen, ob 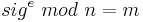 gilt.
gilt.
Wenn man das Signaturprotokoll so anwendet, wie es oben beschrieben ist, ergibt sich das Problem, dass die Signatur die gleiche Länge besitzt, wie das zu unterzeichnende Dokument, was auch bedeutet, dass ein ziemlich hoher Zeitbedarf zur Signierung nötig ist.
Der Vorteil bei dem Verfahren ist jedoch, dass sogenanntes „Message Recovery“ besteht. Dies bedeutet, dass die Originalnachricht bei der Verifizierung aus der Signatur wieder gewonnen werden kann.
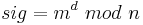
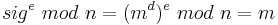
RSA wird gewöhnlich in Blöcken verschlüsselt, da für die Nachricht m gelten muss m < n. Mallory hat daher unter Umständen die Möglichkeit, einzelne Blöcke der Signatur zu entfernen, so dass sich beim Entschlüsseln dennoch ein sinnvoller, vermutlich aber sinnentstellter Text ergibt. Der Angriff ist also noch nicht abgewehrt.
Eine mögliche Lösung für das Problem besteht in der Verwendung von sog. Hashfunktion, mit deren Hilfe es möglich ist, Nachrichten nahezu beliebiger Länge auf eine durch die Hashfunktion festgelegte Größe zusammenzufassen. Dieses Zusammenfassen kann auch als „message digest“ bezeichnet werden.
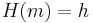
Anschließend sollte der gebildete Hashwert, also die gehashte Nachricht mit oben beschriebenem Protokoll signiert werden, was dank der Kürze der kryptographischen Prüfsumme meist deutlich schneller möglich ist und überdies noch Speicherplatz spart. Dieses
Vorgehen kann man als Hash-and-Sign-Verfahren bezeichnen.
Wichtig ist hierbei zu erwähnen, dass es sich bei Hashfunktion vermutlich um Einwegfunktionen handelt, die nicht effizient umkehrbar sind.
Folglich sollte Alice neben dem signierten Hashwert auch die ursprüngliche Nachricht (Urbild) an Bob senden.
Nach dem Erhalt der Nachricht von Alice empfiehlt es sich für Bob zunächst die Signatur von Alice zu verifizieren. Dazu kann Bob die Signatur mit Alices öffentlichem Schlüssel dechiffrieren, worauf er den Signaturhashwert erhält. Um zu überprüfen, ob die Originalnachricht oder die Signatur von Mallory verändert wurde, hat er die Möglichkeit, aus dem unverschlüsselten Klartext ebenfalls einen Hashwert zu bilden. Dazu sollte Bob, um ein verwertbares Ergebnis zu erhalten, die gleiche Hashfunktion, die auch Alice verwendet hat, anwenden. Die Information, welche Hashfunktion von Alice verwendet wurde, ist in der Regel neben dem Hashwert in der Signatur enthalten. Anschließend kann Bob die Hashwerte vergleichen. Stimmen sie überein, wurde nichts verändert.
Die Hashfunktion SHA-1 (Secure Hash Algorithm), die einen Hashwert von 160 Bit erzeugt, wird heutzutage häufig bei der digitalen Signatur eingesetzt.

