Fermat Faktorisierung: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Die Seite wurde neu angelegt: ===Fermat’sche Faktorisierung=== <br> <math>N = a^2 - b^2 =\underbrace {(a+b)}_{=p}\cdot \underbrace {(a-b)}_{= q} = p\cdot q</math><br><br> ...) |
Version vom 12. September 2010, 09:32 Uhr
Fermat’sche Faktorisierung
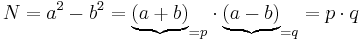
Die Idee des Algorithmus besteht darin, nach Zahlen a und b zu suchen, die die obige Gleichung erfüllen. Meist beginnt man mit ![a = [\sqrt{n} + 1]](/images/math/8/4/9/849e2325d6755f712177b7dacf3a06a1.png)
und erhöht darauf die Zahl a schrittweise um 1 bis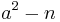 
Quadratzahl ist. Ist diese Forderung erfüllt, so lässt sich zunächst b und dann auch p und q berechnen, womit die Faktorisierung geglückt wäre. In der Praxis gilt dies jedoch für große Moduli n immer noch als nicht effizient berechenbar. Diese und ähnliche Vorgehen werden von Wissenschaftlern und Hackern weltweit verwendet, um die Faktorisierung von n zu brechen oder ein noch effektiveres Verfahren zu entwickeln.
vgl. [7, S.328]
