Facharbeit Lernpfad Terme/Addieren und Subtrahieren von Termen: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
K (→‎Äquivalente Terme)
K (→‎Äquivalente Terme)
Zeile 24: Zeile 24:
  
 
<popup name="Lösung">
 
<popup name="Lösung">
 +
 
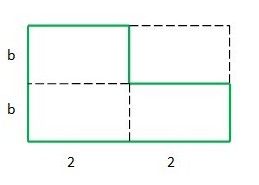
1. Möglichkeit: Man rechnet den Flächeninhalt des gesamten Rechtecks aus 2b•4 und zieht den Flächeninhalt des kleinen Rechtecks 2b ab. Also: A<sub>1</sub> (b)= 2b•4-2b
 
1. Möglichkeit: Man rechnet den Flächeninhalt des gesamten Rechtecks aus 2b•4 und zieht den Flächeninhalt des kleinen Rechtecks 2b ab. Also: A<sub>1</sub> (b)= 2b•4-2b
  
 
2. Möglichkeit: Man rechnet den Flächeninhalt eines kleinen Rechtecks aus 2b und nimmt ihn mal drei. Also A<sub>2</sub> (b)= 3•2b
 
2. Möglichkeit: Man rechnet den Flächeninhalt eines kleinen Rechtecks aus 2b und nimmt ihn mal drei. Also A<sub>2</sub> (b)= 3•2b
  
−
Bei jeder Einsetzung für b müssen die beiden unterschiedlich aussehenden Terme dasselbe Ergebnis ergeben, weil es lediglich verschiedene Rechenwege zur Berechnung des gleichen Flächeninhalts sind.
+
Bei jeder Einsetzung für b müssen die beiden unterschiedlich aussehenden Terme dasselbe Ergebnis ergeben, weil es lediglich verschiedene Rechenwege zur Berechnung des gleichen Flächeninhalts sind. Diese Terme sind <u>'''gleichwertig'''</u>.
 +
</popup> </div>
 +
 
 +
 
 +
 
 +
<div style="orange:0px; margin-right:90px; border: solid orange; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: red">Erklärung:</span>'''
 +
Zwei Terme, die bei jeder möglichen Einsetzung einer Zahl für die Variable jeweils den gleichen Wert annehmen heißen <u>'''gleichwertig'''</u> oder <u>'''äquivalent'''</u>.
 +
Durch Anwendung der Rechengesetze kannst du einen Term in einen äquivalenten Term umformen.
 +
 
 +
<span style="color: green"><u>Rechengesetze:</u></span>
 +
 
 +
* '''Kommutativgesetz (KG)''': für alle rationalen Zahlen a, b gilt: 
 +
::a+b = b+a
 +
::a•b = b•a
 +
* '''Assoziativgesetz (AG)''': für alle rationalen Zahlen a, b, c gilt:
 +
::a+(b+c) = (a+b)+c = a+b+c
 +
::a•(b•c) = (a•b)•c = a•b•c
 +
* '''Distributivgesetz (DG)''': für alle rationalen Zahlen a, b, c gilt:
 +
::a•(b+c) = a•b+a•c
 +
:für alle rationalen Zahlen a, b, c (c<math>\neq</math> 0) gilt:
 +
::(b+c):a = b:a+c:a

Version vom 11. August 2010, 14:03 Uhr

Addieren und Subtrahieren von Termen

Äquivalente Terme




Übertrage die Zeichnung in dein Heft und überlege dir zwei verschiedene Terme, mit denen du den Flächeninhalt der grün markierten Fläche ausrechnen kannst.


Tipp: In der vorherigen Aufgabe gab es auch 2 Möglichkeiten den Flächeninhalt zu errechnen.



Einstieg addierensubtrahieren.jpg


Erklärung:

Zwei Terme, die bei jeder möglichen Einsetzung einer Zahl für die Variable jeweils den gleichen Wert annehmen heißen gleichwertig oder äquivalent. Durch Anwendung der Rechengesetze kannst du einen Term in einen äquivalenten Term umformen.

Rechengesetze:

  • Kommutativgesetz (KG): für alle rationalen Zahlen a, b gilt:
a+b = b+a
a•b = b•a
  • Assoziativgesetz (AG): für alle rationalen Zahlen a, b, c gilt:
a+(b+c) = (a+b)+c = a+b+c
a•(b•c) = (a•b)•c = a•b•c
  • Distributivgesetz (DG): für alle rationalen Zahlen a, b, c gilt:
a•(b+c) = a•b+a•c
für alle rationalen Zahlen a, b, c (c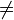\neq 0) gilt:
(b+c):a = b:a+c:a
Von „http://rmg.zum.de/index.php?title=Facharbeit_Lernpfad_Terme/Addieren_und_Subtrahieren_von_Termen&oldid=34299“