Facharbeit Lernpfad Terme/Aufstellen und Interpretieren von Termen: Unterschied zwischen den Versionen
Aus RMG-Wiki
K (→Aufstellen von Termen) |
K |
||
| Zeile 84: | Zeile 84: | ||
[[Bild:termgliederungsbaum2.2.jpg]] | [[Bild:termgliederungsbaum2.2.jpg]] | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
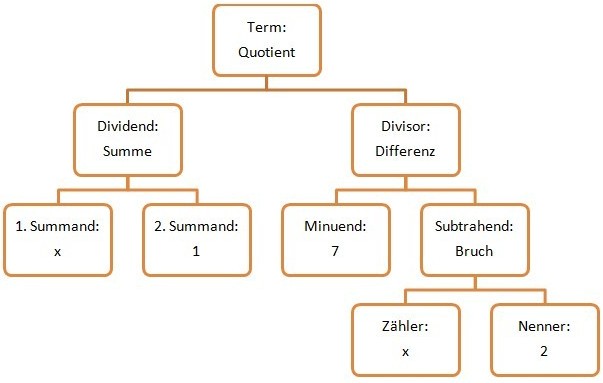
| − | Der Gliederungsbaum ergibt, wenn man seinen Abzweigungen richtig folgt, folgenden Term: T(x)= (x+1):(7-<math>\frac{x}{2}</math>) | + | Der Gliederungsbaum ergibt, wenn man seinen Abzweigungen von oben nach unten richtig folgt, folgenden Term: T(x)= (x+1):(7-<math>\frac{x}{2}</math>) |
T(4)= (4+1):(7-<math>\frac{4}{2}</math>) = 5:(7-2) = 5:5 = 1 | T(4)= (4+1):(7-<math>\frac{4}{2}</math>) = 5:(7-2) = 5:5 = 1 | ||
Version vom 11. August 2010, 08:10 Uhr
Inhaltsverzeichnis |
Aufstellen und Interpretieren von Termen
Aufstellen von Termen
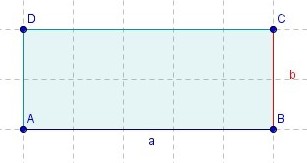
Übertrage die Zeichnung in dein Heft und überlege dir einen Term, mit dem du den Flächeninhalt ausrechnen kannst.
Setze nun für a=2cm und b=3cm ein
Erklärung:
Um Sachverhalte oder Probleme möglichst kurz zu beschreiben erstellt man einen Term. Dabei solltest du so vorgehen:
Um Sachverhalte oder Probleme möglichst kurz zu beschreiben erstellt man einen Term. Dabei solltest du so vorgehen:
Rezept
- Untersuche den Sachverhalt bzw. das Problem und suche nach einer Gesetzmäßigkeit
- Führe eine (oder mehrere) Variable(n) ein
- Stelle den Term auf und überlege dir die zugehörige Definitionsmenge
Beispiel:
Interpretieren von Termen
Erklärung:
|
|
Übungsaufgaben
Aufgabe 1: Übersetze die Rechenvorschrift in einen Term:
a) Addiere 2 zum Quadrat von x
b) Addiere 6 zum vierfachen der Zahl n
c) Multipliziere die Summe aus b und der Zahl 7 mit 4
d) Multipliziere x mit seiner Gegenzahl
e) Multipliziere den Vorgänger der natürlichen Zahl n mit seinem Nachfolger
Aufgabe 2:Gib den Term zu folgendem Gliederungsbaum an und berechne seinen Wert für x=4!
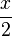 )
)
 ) = 5:(7-2) = 5:5 = 1
) = 5:(7-2) = 5:5 = 1
