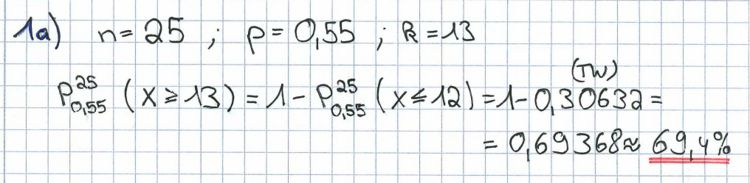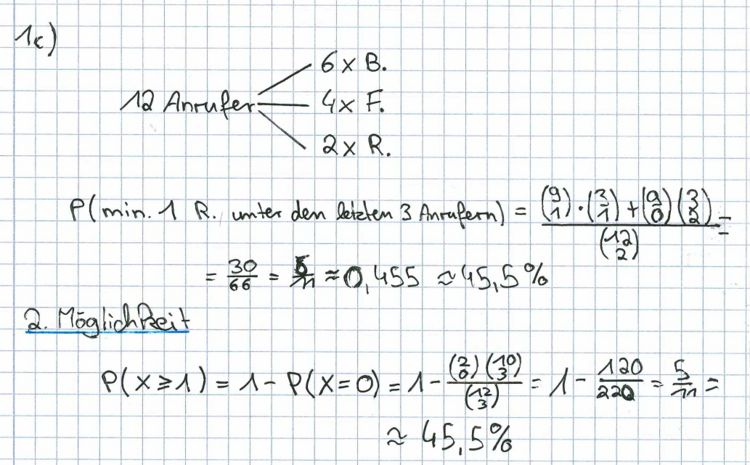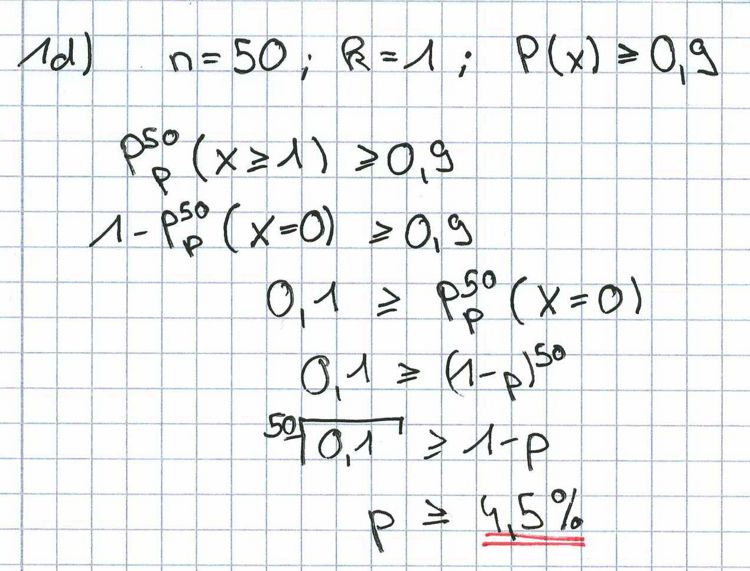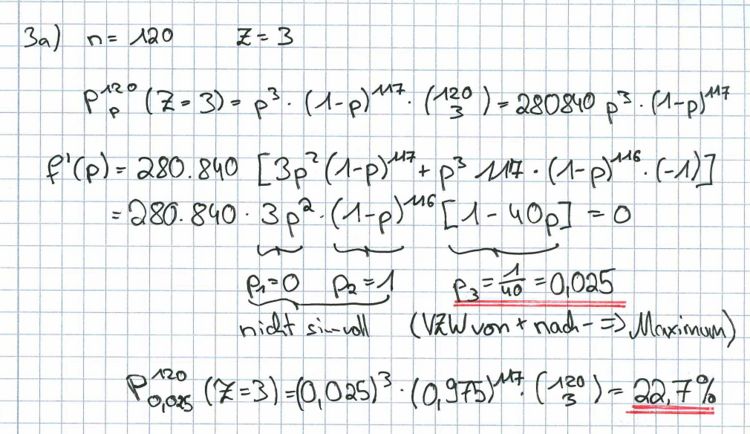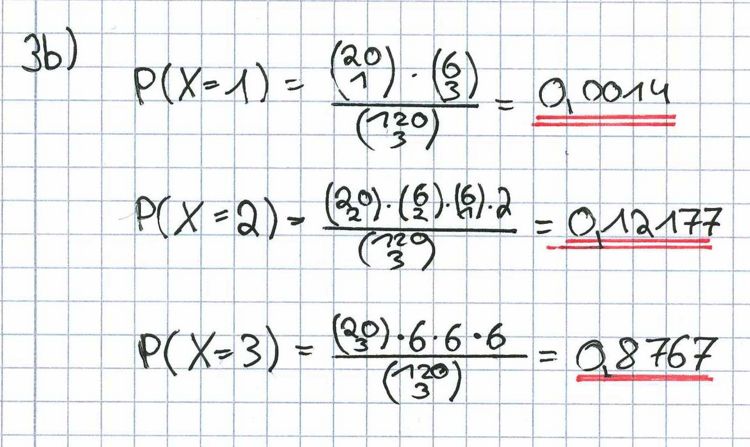2004 III: Unterschied zwischen den Versionen
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| − | <center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung | + | <center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2004'''</big></center> |
<center><big>'''Wahrscheinlichkeitsrechnung/Statistik III'''</big></center> | <center><big>'''Wahrscheinlichkeitsrechnung/Statistik III'''</big></center> | ||
| Zeile 117: | Zeile 117: | ||
b) Die Zufallsgröße X bezeichne die Anzahl der Gruppen, bei denen der Erreger bei der Untersuchung der Blutgemische gefunden wird. Sie hat folgende Verteilung: | b) Die Zufallsgröße X bezeichne die Anzahl der Gruppen, bei denen der Erreger bei der Untersuchung der Blutgemische gefunden wird. Sie hat folgende Verteilung: | ||
| − | [[Bild:Stochastik04IIITabelle.jpg]] | + | [[Bild:Stochastik04IIITabelle.jpg|750px]] |
Weisen Sie nach, dass die beiden angegebenen (gerundeten) Wahrscheinlichkeiten richtig sind, und berechnen Sie den dritten Wert. | Weisen Sie nach, dass die beiden angegebenen (gerundeten) Wahrscheinlichkeiten richtig sind, und berechnen Sie den dritten Wert. | ||
Aktuelle Version vom 12. April 2010, 14:27 Uhr
|
|
1. Im Mittel wollen 55 % der Anrufer des Callcenters eines großen Touristikunternehmens eine Reise buchen, während 27 % Fragen zu bereits gebuchten Reisen haben. Die restlichen Anrufer haben verschiedene andere Anliegen.
3BE
3BE
5BE
5BE
|
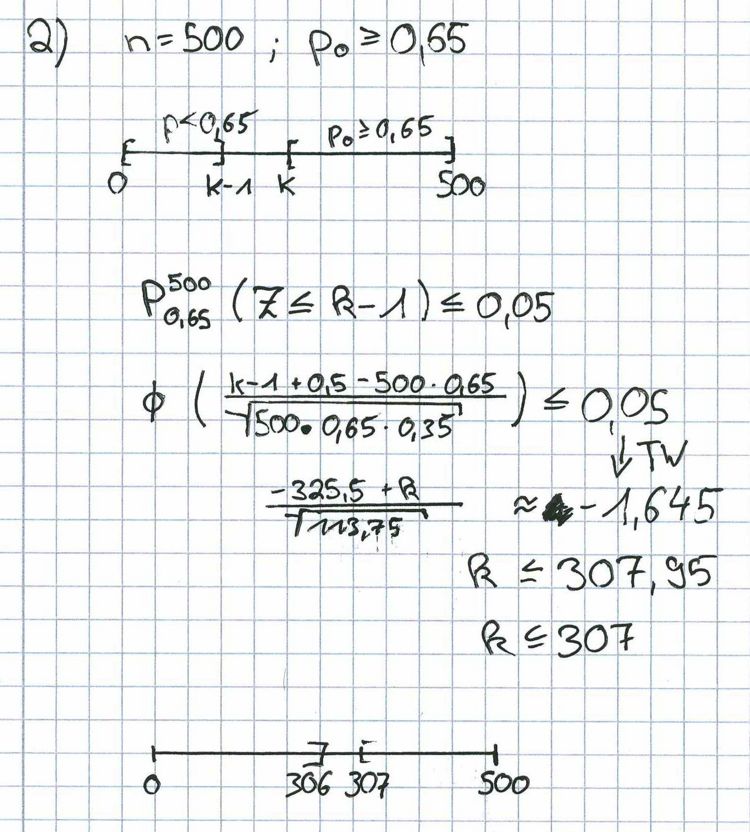
2. Der Vorstand des Touristikunternehmens beabsichtigt, eine Buchungs-möglichkeit über das Internet einzurichten. Die Geschäftsführung vertritt jedoch die Meinung, dass sich diese Investition nicht lohnt. Um zu testen, ob die Vermutung der Geschäftsführung zutrifft, werden 500 zufällig ausgewählte Kunden bei der Buchung einer Reise befragt. Bestimmen Sie mit Hilfe der Normalverteilung die Entscheidungsregel für die Nullhypothese „Mindestens 65 % der Kunden ziehen die herkömmlichen Buchungsmöglichkeiten einer Buchung über das Internet vor“ auf dem Signifikanzniveau von 5 %. 7BE
|