2006 II: Unterschied zwischen den Versionen
| Zeile 29: | Zeile 29: | ||
:: <math>f_k = \frac{k}{1+e^{-kx}}</math> <br /> | :: <math>f_k = \frac{k}{1+e^{-kx}}</math> <br /> | ||
mit <math>k \in IR^{+}</math> und Definitionsmenge <math>IR \,</math>. <math>G_k \,</math> bezeichnet den Graphen von <math>f_k \,</math>. | mit <math>k \in IR^{+}</math> und Definitionsmenge <math>IR \,</math>. <math>G_k \,</math> bezeichnet den Graphen von <math>f_k \,</math>. | ||
| + | |||
| + | |||
a) Untersuchen Sie das Verhalten von <math>f_k \,</math> für <math>x \rightarrow +\infty</math> und <math>x \rightarrow -\infty</math>. | a) Untersuchen Sie das Verhalten von <math>f_k \,</math> für <math>x \rightarrow +\infty</math> und <math>x \rightarrow -\infty</math>. | ||
| Zeile 36: | Zeile 38: | ||
}} | }} | ||
| − | b) Bestimmen Sie das Monotonieverhalten von | + | b) Bestimmen Sie das Monotonieverhalten von <math>f_k \,</math> und geben Sie die Wertemenge an. |
| − | [mögliches Zwischenergebnis: | + | [mögliches Zwischenergebnis: f_k ^{'}(x)= ] |
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| Zeile 43: | Zeile 45: | ||
}} | }} | ||
| − | c) Weisen Sie nach, dass der Punkt | + | c) Weisen Sie nach, dass der Punkt <math>W_k (0/\frac{k}{2})</math> der einzige Wendepunkt von <math>G_k \,</math> ist. |
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| Zeile 49: | Zeile 51: | ||
}} | }} | ||
| − | d) Weisen Sie nach, dass für alle | + | d) Weisen Sie nach, dass für alle <math>k \in IR+</math> und alle <math>x \in IR</math> gilt: <math>f_k(-x) + f_k(x)=k \,</math>. Begründen Sie damit die Symmetrie von <math>G_k \,</math> zum Punkt <math>W_k \,</math> . |
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| Zeile 55: | Zeile 57: | ||
}} | }} | ||
| − | e) Die beiden Koordinatenachsen und | + | e) Die beiden Koordinatenachsen und <math>G_k \,</math> begrenzen im zweiten Quadranten ein sich ins Unendliche erstreckendes Flächenstück. Veranschaulichen Sie dieses Flächenstück in einer Skizze. Zeigen Sie, dass das Flächenstück den endlichen Inhalt <math>\ln (2)</math> besitzt. |
| − | (Hinweis: Für die Integration ist es hilfreich, den Funktionsterm mit zu erweitern.) | + | (Hinweis: Für die Integration ist es hilfreich, den Funktionsterm mit <math>e^{kx}</math> zu erweitern.) |
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
Version vom 18. Februar 2010, 16:11 Uhr
|
|
1.Gegeben ist die Schar der Funktionen mit
a) Untersuchen Sie das Verhalten von
b) Bestimmen Sie das Monotonieverhalten von
c) Weisen Sie nach, dass der Punkt
d) Weisen Sie nach, dass für alle
e) Die beiden Koordinatenachsen und
|
2. Bei vielen Wachstumsvorgängen ist kein unbeschränktes Wachstum möglich. Dies gilt z. B. auch für eine Bakterienkultur, deren Bakterienzahl schließlich einer oberen Grenze entgegenstrebt. Die Zahl der Bakterien einer Kultur wird näherungsweise durch die Funktion N mit , beschrieben. Dabei gibt x die Zeit in Stunden an, die seit dem Ansetzen der Bakterienkultur vergangen ist. Die Abbildung zeigt den Graphen von N. a) Geben Sie an, wie der Graph von N aus der Aufgabe 1 entsteht.
b) Mit wie vielen Bakterien wurde die Kultur angesetzt, wie viele Bakterien sind es nach zwei Stunden?
c) Berechnen Sie, nach welcher Zeit 90 % des Grenzbestandes von 2 Millionen Bakterien erreicht sind.
d) Schätzen Sie rechnerisch ab, wie viele Bakterien in der Minute stärksten Wachstums hinzukommen.
|
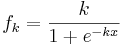
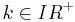 und Definitionsmenge
und Definitionsmenge 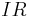 .
. 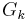 bezeichnet den Graphen von
bezeichnet den Graphen von 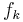 .
.
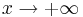 und
und 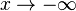 .
.
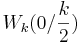 der einzige Wendepunkt von
der einzige Wendepunkt von 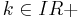 und alle
und alle 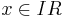 gilt:
gilt: 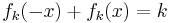 . Begründen Sie damit die Symmetrie von
. Begründen Sie damit die Symmetrie von 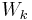 .
.
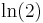 besitzt.
(Hinweis: Für die Integration ist es hilfreich, den Funktionsterm mit
besitzt.
(Hinweis: Für die Integration ist es hilfreich, den Funktionsterm mit 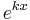 zu erweitern.)
zu erweitern.)

