2008 VI: Unterschied zwischen den Versionen
Aus RMG-Wiki
< LK Mathematik | Abitur
(Die Seite wurde neu angelegt: Inhalt folgt) |
(bis Aufgabe 1 a) |
||
| Zeile 1: | Zeile 1: | ||
| − | + | __NOTOC__ | |
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | <center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2008'''</big></center> | ||
| + | <center><big>'''Geometrie VI'''</big></center> | ||
| + | |||
| + | |||
| + | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=6765c5a90ce67dce2877992c3f4e2d9f '''Download der Originalaufgaben: Abitur 2008 LK Mathematik Bayern'''] - [[Media:LKM Abi 2008 VI lös.doc|Lösungen zum Ausdrucken]]</center> | ||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 1 | ||
| + | |||
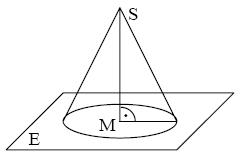
| + | In einem kartesischen Koordinatensystem des IR<sup>3</sup> sind die Punkte M(−2|4|1), S(6|8|9), P(4|−8|1) sowie die Gerade g : <math>\vec x = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} + \lambda\begin{pmatrix} -1 \\ 0 \\ 1 \end{pmatrix}</math>, λ ∈ IR gegeben. | ||
| + | Die Strecke [MS] ist die Höhe eines geraden Kreiskegels. Sein Grundkreis k um den Punkt M hat den Radius <math>6\sqrt{5}</math> und liegt in der Ebene E. | ||
| + | <br /> [[Bild:Beispiel.jpg]] | ||
| + | |||
| + | a) Ermitteln Sie eine Gleichung der Ebene E in Normalenform und zeigen Sie, dass der Punkt P auf dem Grundkreis k liegt. | ||
| + | <br />[Zur Kontrolle: E : 2x1 + x2 + 2x3 − 2 = 0] | ||
| + | |||
| + | [[Bild:ABI_2008_VI_Grafik_A1.jpg]] | ||
| + | |||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:ABI_2009_III_1a_Lös.jpg|750px]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | b) Die Wahrscheinlichkeit für eine fehlerhafte Fliese sei p. Wie würde die Entscheidungsregel mit einem möglichst großen Ablehnungsbereich lauten, wenn man die Nullhypothese H<sub>0</sub>: p > 0,1 anhand der 50 Fliesen eines Kartons auf dem Signifikanzniveau 5 % testen würde? | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:ABI_2009_III_1b_Lös.jpg|750px]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 2 | ||
| + | |||
| + | |||
| + | <popup name="Tipp"> | ||
| + | ''hier könnt könnte eine Formel,ein Hinweis auf Wesentliches, Links zu Hilfeseiten usw...stehen'' | ||
| + | </popup> | ||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
Version vom 5. Februar 2010, 12:09 Uhr
|
|
In einem kartesischen Koordinatensystem des IR3 sind die Punkte M(−2|4|1), S(6|8|9), P(4|−8|1) sowie die Gerade g : a) Ermitteln Sie eine Gleichung der Ebene E in Normalenform und zeigen Sie, dass der Punkt P auf dem Grundkreis k liegt.
|
|
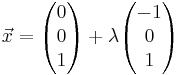 , λ ∈ IR gegeben.
Die Strecke [MS] ist die Höhe eines geraden Kreiskegels. Sein Grundkreis k um den Punkt M hat den Radius
, λ ∈ IR gegeben.
Die Strecke [MS] ist die Höhe eines geraden Kreiskegels. Sein Grundkreis k um den Punkt M hat den Radius 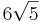 und liegt in der Ebene E.
und liegt in der Ebene E.