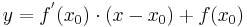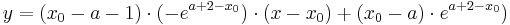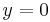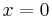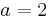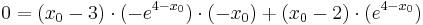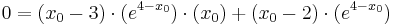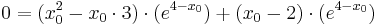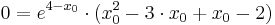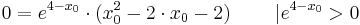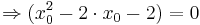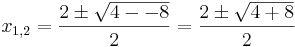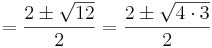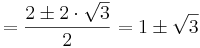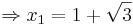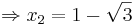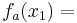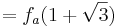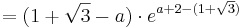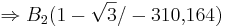Lösung von Teilaufgabe c) 2.: Unterschied zwischen den Versionen
Aus RMG-Wiki
(→Verwendung der Tangentialgleichung) |
(→Verwendung der Tangentengleichung) |
||
| Zeile 4: | Zeile 4: | ||
=== Verwendung der Tangentengleichung === | === Verwendung der Tangentengleichung === | ||
Hier rate ich wieder zur Verwendung der Tangentengleichung.<br /> | Hier rate ich wieder zur Verwendung der Tangentengleichung.<br /> | ||
| − | + | ||
: <math>y = f^{'}( x_0)\cdot ( x - x_0 ) + f ( x_0 )</math><br /> | : <math>y = f^{'}( x_0)\cdot ( x - x_0 ) + f ( x_0 )</math><br /> | ||
| + | Zwar fehlen hier einige feste Werte die man in die Gleichung einsetzen könnte, dochdiese hat man in allgemeiner Form durch die Funktion und die Ableitung gegeben.<br /> | ||
:<math> y = ( x_0 - a - 1 )\cdot ( -e^{a + 2 - x_0})\cdot ( x - x_0 ) + ( x_0 - a )\cdot e^{a + 2 - x_0})</math><br /> | :<math> y = ( x_0 - a - 1 )\cdot ( -e^{a + 2 - x_0})\cdot ( x - x_0 ) + ( x_0 - a )\cdot e^{a + 2 - x_0})</math><br /> | ||
| Zeile 28: | Zeile 29: | ||
:: <math>\Rightarrow ( x_0^{2} - 2\cdot x_0 - 2 ) = 0</math> | :: <math>\Rightarrow ( x_0^{2} - 2\cdot x_0 - 2 ) = 0</math> | ||
| − | + | ||
| + | Nun hat man als Lösung eine Quadratische Gleichung erhalten. Diese löst man am besten mit Hilfe der Mitternachtsformel. | ||
Lösen quadratischer Gleichungen mit Hilfe der [http://de.wikipedia.org/wiki/Mitternachtsformel?title=Mitternachtsformel&redirect=no Mitternachtsformel] <math> x_{1,2} = \frac{-b\pm\sqrt{b^{2}-4\cdot a\cdot c}}{2a}</math> | Lösen quadratischer Gleichungen mit Hilfe der [http://de.wikipedia.org/wiki/Mitternachtsformel?title=Mitternachtsformel&redirect=no Mitternachtsformel] <math> x_{1,2} = \frac{-b\pm\sqrt{b^{2}-4\cdot a\cdot c}}{2a}</math> | ||
Version vom 26. Januar 2010, 18:49 Uhr
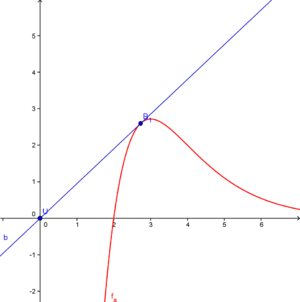
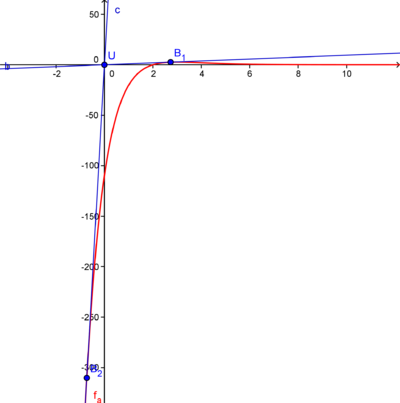
Berechnung derjenigen Punkte, für welche die Tangente an den Graphen von f2 durch den Ursprung verläuft
Verwendung der Tangentengleichung
Hier rate ich wieder zur Verwendung der Tangentengleichung.
Zwar fehlen hier einige feste Werte die man in die Gleichung einsetzen könnte, dochdiese hat man in allgemeiner Form durch die Funktion und die Ableitung gegeben.
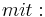
Nun hat man als Lösung eine Quadratische Gleichung erhalten. Diese löst man am besten mit Hilfe der Mitternachtsformel.
Lösen quadratischer Gleichungen mit Hilfe der Mitternachtsformel 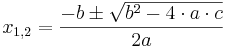
Fehler beim Erstellen des Vorschaubildes: Ungültige Thumbnail-Parameter