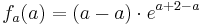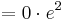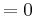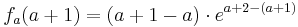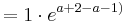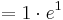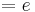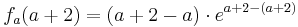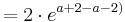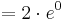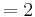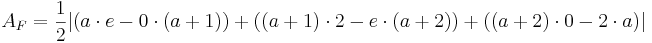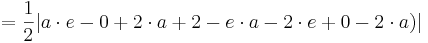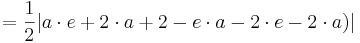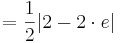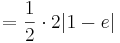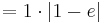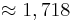Lösung von Teilaufgabe d: Unterschied zwischen den Versionen
(→Kongruenz der Dreiecke) |
|||
| Zeile 1: | Zeile 1: | ||
== Kongruenz der Dreiecke == | == Kongruenz der Dreiecke == | ||
| − | Die Dreiecke werden durch die Punkte <math>\; R_a\;( a / f_a (a))</math>, <math>H_a\; ( a + | + | Die Dreiecke werden durch die Punkte <math>\; R_a\;( a / f_a (a))</math>, <math>H_a\; ( a + 2 / f_a ( a + 2 ))</math> und <math>H_a\; ( a + 1 / f_a ( a + 1 ))</math> festgelegt. |
| Zeile 51: | Zeile 51: | ||
<ggb_applet width="773" height="412" version="3.2" ggbBase64="UEsDBBQACAAIAFmkNzwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s5VjbbuM2EH3ufgWhpxZd27pYvgB2Fu0WxQZIm6LZ7gJ9KWhpbLORSFekYjnf0z/pj3V4kSzf0jjtBlk0QCCJHA1nzjkzpDx5U+UZuYNCMsGnXtD1PQI8ESnji6lXqnln5L25eDVZgFjArKBkLoqcqqkXdUNPj5fs4tUXE7kUa0IzY/KBwXrqqaIEj8hVATSVSwBlh+c0kzhOy4pljBab69nvkCi5nbA+LvmqVLWTJE+vmKwfe2a9VcbUd+yOpVCQTCRTbxBj5Hj3AQrFEppNvb5vR0JMa7A7iUORnl2Kgt0LrrT51vkcRwiR7B7wzVCPTXomzwmUScZSRrlOxsSBRoSsWaqWGII/RJfAFkuMtR/41lsiRJHebKSCnFS/QiGmXhjEGueNfYrsk8S4cMHYN1PtJ+MG7m5AKWRFElqBrLFZFCxtwNMPl/JbkW2HVoJx9ZauVFkYRiM3dKM22j8uVeh4v+GLDNxYiIgvIbmdierGYhBZ1+83K/OKiWe2eCsyUZACX4hjNHDXmb0aGx1oY+UbG99YOB/aaTMfjENjYa4zezVWGeM2NJd4UGddI0wrJoke0CiiEGtsMjoDJNYjJWfqqn5AAdy6TANr/2OZz7AA2hJoXAb/kctJb087k1soOGRWIRyJLUUpyZ1WoqXOxJFCwnJ8tBMOEKrJ+gUDsKMpLAqo47blY+Eyszsq3Bue9OogdAwSY00UtgHMR+lcdJkqLBF9l1KlR3QNZJADFogyauBlDgVLGmSop1fDJUq3UNCNXMnqFiFMue+huYUdp0/oBRvDaknxrhs4VdANln47RePtB5HWC7tlM9MjcobdrWMKLacVFpa+ozMpslLBTYIA8iuRUGW6oI3OVXXgm4qsdMswpVnX6JxVsC20461kq121RJFwkNIUmGqXEuXIsQEem8TK5oidE8Dqr7YlK8zZFHEjEFSVZUPzUmGvlbqN17j+/BvFZl6hxy/pa4Ixf1U7My3AI70DOt1Ey8G/pc40hYY8/5HktVUrNfZaRhp6g/y93aiMie1mug2bF6MDWB6UK+zLNewOg1E40v/9eOz34yPidYw/h3qNxuxIqznVm+fuxMNieNcSA/maIH6vCZwriHcvRxChE8QhYefJ4wCoj7tAhRqo8Pza+fhyoIoaqM6snUTkOeUp4TTH/H4S2WYhuMmK6fMZob5rMjRwAqOhzdymVara6vvsrz/xUMEZX9JM2RfW9QuFuYmm3tK+Oem5hY9AbEOoIdxz++iOe5qU1t7bZiWII8NLHJxZ0dfzuQRlBDu2JISnSTvdtyQs9FMT5tqp69mzfViE22w7/cCkO3icRDtHyth0+/Hu38gIOOrGUTQcDPB/PB4M49HwjN0W/uDWRtoTG8vxWyJhqtFspjfZS67w/AbmPHR4LLsFWOnT8DV/X1Au9TfRA734QSaLl85kYJtHJxg9jkp/n0krhMA1n06/Gw39CD+/omgc9Ef98efL3fIz4S6MH7un+o7r43WHVTp40WwdbOYzt5VvyJTAsU1bJ+JtrT8dm6cOhE/e1euPkaawThxdn0QVgtZQdboedsBLXj54T//Q+gfg/eeFOv2/Qu1/EqR77R8/zI997sfOi78BUEsHCJ4zfji5BAAAHhUAAFBLAQIUABQACAAIAFmkNzyeM344uQQAAB4VAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAA8wQAAAAA" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /><br /><br /> | <ggb_applet width="773" height="412" version="3.2" ggbBase64="UEsDBBQACAAIAFmkNzwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s5VjbbuM2EH3ufgWhpxZd27pYvgB2Fu0WxQZIm6LZ7gJ9KWhpbLORSFekYjnf0z/pj3V4kSzf0jjtBlk0QCCJHA1nzjkzpDx5U+UZuYNCMsGnXtD1PQI8ESnji6lXqnln5L25eDVZgFjArKBkLoqcqqkXdUNPj5fs4tUXE7kUa0IzY/KBwXrqqaIEj8hVATSVSwBlh+c0kzhOy4pljBab69nvkCi5nbA+LvmqVLWTJE+vmKwfe2a9VcbUd+yOpVCQTCRTbxBj5Hj3AQrFEppNvb5vR0JMa7A7iUORnl2Kgt0LrrT51vkcRwiR7B7wzVCPTXomzwmUScZSRrlOxsSBRoSsWaqWGII/RJfAFkuMtR/41lsiRJHebKSCnFS/QiGmXhjEGueNfYrsk8S4cMHYN1PtJ+MG7m5AKWRFElqBrLFZFCxtwNMPl/JbkW2HVoJx9ZauVFkYRiM3dKM22j8uVeh4v+GLDNxYiIgvIbmdierGYhBZ1+83K/OKiWe2eCsyUZACX4hjNHDXmb0aGx1oY+UbG99YOB/aaTMfjENjYa4zezVWGeM2NJd4UGddI0wrJoke0CiiEGtsMjoDJNYjJWfqqn5AAdy6TANr/2OZz7AA2hJoXAb/kctJb087k1soOGRWIRyJLUUpyZ1WoqXOxJFCwnJ8tBMOEKrJ+gUDsKMpLAqo47blY+Eyszsq3Bue9OogdAwSY00UtgHMR+lcdJkqLBF9l1KlR3QNZJADFogyauBlDgVLGmSop1fDJUq3UNCNXMnqFiFMue+huYUdp0/oBRvDaknxrhs4VdANln47RePtB5HWC7tlM9MjcobdrWMKLacVFpa+ozMpslLBTYIA8iuRUGW6oI3OVXXgm4qsdMswpVnX6JxVsC20461kq121RJFwkNIUmGqXEuXIsQEem8TK5oidE8Dqr7YlK8zZFHEjEFSVZUPzUmGvlbqN17j+/BvFZl6hxy/pa4Ixf1U7My3AI70DOt1Ey8G/pc40hYY8/5HktVUrNfZaRhp6g/y93aiMie1mug2bF6MDWB6UK+zLNewOg1E40v/9eOz34yPidYw/h3qNxuxIqznVm+fuxMNieNcSA/maIH6vCZwriHcvRxChE8QhYefJ4wCoj7tAhRqo8Pza+fhyoIoaqM6snUTkOeUp4TTH/H4S2WYhuMmK6fMZob5rMjRwAqOhzdymVara6vvsrz/xUMEZX9JM2RfW9QuFuYmm3tK+Oem5hY9AbEOoIdxz++iOe5qU1t7bZiWII8NLHJxZ0dfzuQRlBDu2JISnSTvdtyQs9FMT5tqp69mzfViE22w7/cCkO3icRDtHyth0+/Hu38gIOOrGUTQcDPB/PB4M49HwjN0W/uDWRtoTG8vxWyJhqtFspjfZS67w/AbmPHR4LLsFWOnT8DV/X1Au9TfRA734QSaLl85kYJtHJxg9jkp/n0krhMA1n06/Gw39CD+/omgc9Ef98efL3fIz4S6MH7un+o7r43WHVTp40WwdbOYzt5VvyJTAsU1bJ+JtrT8dm6cOhE/e1euPkaawThxdn0QVgtZQdboedsBLXj54T//Q+gfg/eeFOv2/Qu1/EqR77R8/zI997sfOi78BUEsHCJ4zfji5BAAAHhUAAFBLAQIUABQACAAIAFmkNzyeM344uQQAAB4VAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAA8wQAAAAA" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /><br /><br /> | ||
<br /> | <br /> | ||
| − | |||
| − | |||
| − | |||
== Flächeninhalt des Dreiecks == | == Flächeninhalt des Dreiecks == | ||
Version vom 24. Januar 2010, 16:06 Uhr
Inhaltsverzeichnis[Verbergen] |
Kongruenz der Dreiecke
Die Dreiecke werden durch die Punkte 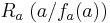 ,
, 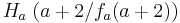 und
und 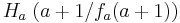 festgelegt.
festgelegt.
1.Punkt : 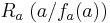
Der Punkt Ra liegt für alle a bei Ra ( a / 0 )
2.Punkt : 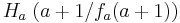
Der Punkt Ha liegt für alle a bei Ha ( a + 1 / e )
3.Punkt : 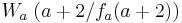
Der Punkt Wa liegt für alle a bei Wa ( a + 2 / 2 )
Mit den nun drei bestimmten Punkten Ra, Ha und Wa lässt sich sagen, dass die Dreiecke kongruent sein müssen. Die y-Werte aller drei Punkte sind für alle a identisch. Daraus schließt man, dass sich die drei Punkte nur auf der x-Achse beziehungsweise auf einer Parallelen zur x-Achse, immer um den gleichen Wert, nämlich um a, verschieben lassen. Da sich die Punkte nur auf Parallelen zur x-Achse verschieben, heißt das natürlich auch, dass sich das Dreieck nur auf der x-Achse verschieben kann und somit immer kongruent ist.
Flächeninhalt des Dreiecks
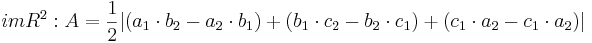
siehe Formelsammlung Seit 81
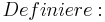
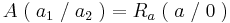
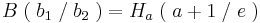
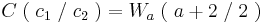
Der Flächeninhalt beträgt, unabhängig von a, | 1 - e |