Der Holzweg: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Die Seite wurde neu angelegt: df) |
|||
| Zeile 1: | Zeile 1: | ||
| − | + | <math> \int_{a}^{b} f_a ( x )\,dx = ( x - a ) e^{a + 2 - x}</math> | |
| + | |||
| + | Definiere: | ||
| + | |||
| + | <math>v ^{'} ( x ) = x - a\,</math><br /><br /> | ||
| + | <math>v ( x ) = \frac{x^{2}}{2}-a\cdot x</math><br /> | ||
| + | <math>u ( x ) = e^{a + 2 - x}\,</math><br /><br /> | ||
| + | <math>u ^{'} ( x ) = -e^{a + 2 - x}\,</math><br /> | ||
| + | |||
| + | |||
| + | <math> \int_{a}^{b} f_a ( x )\,dx = ( x - a )\cdot e^{a + 2 - x}</math> <br /> | ||
| + | ::: <math>=[( \frac{x^{2}}{2}-a\cdot x )\cdot e^{a + 2 - x} ]^{b}_{a} - \int_{a}^{b} ( \frac{x^{2}}{2}-a\cdot x ) \cdot (-e^{a + 2 - x})\,dx</math> | ||
| + | |||
| + | |||
| + | |||
| + | : <math>\Rightarrow</math> Man kommt zu keiner sinnenvollen Loesung fuer dieses Integral, da aus dem <math>\int_{a}^{b} x\cdot e^{a + 2 - x}\,dx</math> ein <math>\int_{a}^{b}( \frac{x^{2}}{2}-a\cdot x )\cdot e^{a + 2 - x}\,dx</math> geworden ist. | ||
Version vom 23. Januar 2010, 21:47 Uhr
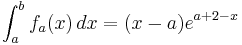
Definiere:
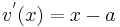
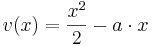
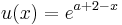
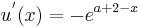
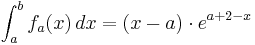
-
 Man kommt zu keiner sinnenvollen Loesung fuer dieses Integral, da aus dem
Man kommt zu keiner sinnenvollen Loesung fuer dieses Integral, da aus dem 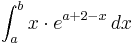 ein
ein 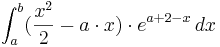 geworden ist.
geworden ist.
![=[( \frac{x^{2}}{2}-a\cdot x )\cdot e^{a + 2 - x} ]^{b}_{a} - \int_{a}^{b} ( \frac{x^{2}}{2}-a\cdot x ) \cdot (-e^{a + 2 - x})\,dx](/images/math/e/3/3/e3398c601783131efc32419d8e9064a6.png)

