Messwerte: Unterschied zwischen den Versionen
(GeoGebra eingefügt) |
|||
| Zeile 72: | Zeile 72: | ||
Julian Rudolph, Felix Göller, Markus Fischer: | Julian Rudolph, Felix Göller, Markus Fischer: | ||
| − | + | ||
| + | Benötigte Materialien: | ||
| + | :-Metermaß | ||
| + | :-Schnur | ||
| + | :-Gewichtsstück(e) | ||
| + | :-Stopuhr | ||
| + | :-Haken zum Befestigen | ||
| + | |||
| + | Durchführung: | ||
| + | |||
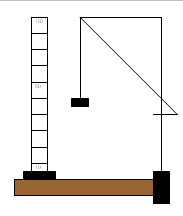
| + | Zuerst hängt man die Schnur mit dem Gewichtsstück an den Haken vom Stab. | ||
| + | Dann misst man erst 10cm Schnurlänge. Nun lenkt man das Gewichtsstück | ||
| + | mit der Schnur um etwa 20° vom Stab weg aus der senkrechten, und lassen es dann los. | ||
| + | Ab diesem Moment messen wir 10 Schwingungen. | ||
| + | |||
| + | Dann macht man das gleiche mit 20cm, 30cm, 40cm, 50cm. | ||
| + | |||
| + | Die Auslenkung muss nicht genau 20° sein, sie kann auch nur 10° sein, | ||
| + | das Ergebnis (Schwingungsdauer ist die selbe). Auch wieviel Gewicht an der | ||
| + | Schnur hängt spielt keine Rolle. Vielleicht würde mehr Gewicht die Reibung | ||
| + | erhöhen und dadurch die Messwerte nochmehr verfälschen... | ||
| + | |||
| + | |||
{| class="wikitable sortable" | {| class="wikitable sortable" | ||
| Zeile 78: | Zeile 100: | ||
| Pendellänge l in cm || Schwingungsdauer T in s | | Pendellänge l in cm || Schwingungsdauer T in s | ||
|- | |- | ||
| − | | 10|| | + | | 10|| 6,3 |
|- | |- | ||
| − | | 20 || | + | | 20 || 9,0 |
|- | |- | ||
| − | | 30 || | + | | 30 || 11,0 |
|- | |- | ||
| − | | 40 || | + | | 40 || 12,6 |
|- | |- | ||
| − | | 50 || | + | | 50 || 14,2 |
|- | |- | ||
|} | |} | ||
| + | Daraus ergibt sich pro Schwingung eine Zeit von: | ||
| + | :Für 10 cm: 0,63s | ||
| + | :Für 20 cm: 0,90s | ||
| + | :Für 30 cm: 1,10s | ||
| + | :Für 40 cm: 1,26s | ||
| + | :Für 50 cm: 1,42s | ||
Anmerkungen: | Anmerkungen: | ||
| + | |||
| + | Für 10 cm: Fallbeschleunigung g = 9,95 m/s<sup>2</sup> | ||
Für 20 cm: Fallbeschleunigung g = 9,74 m/s<sup>2</sup> | Für 20 cm: Fallbeschleunigung g = 9,74 m/s<sup>2</sup> | ||
| + | |||
| + | Für 30 cm: Fallbeschleunigung g = 9,79 m/s<sup>2</sup> | ||
| + | |||
| + | Für 40 cm: Fallbeschleunigung g = 9,95 m/s<sup>2</sup> | ||
Für 50 cm: Fallbeschleunigung g = 9,79 m/s<sup>2</sup> | Für 50 cm: Fallbeschleunigung g = 9,79 m/s<sup>2</sup> | ||
| − | Die Abweichungen ergeben sich wegen den Messfehlern für die Pendellänge und der Schwingungsdauer. | + | Abweichungen durch folgende Gründe: |
| + | ::-Luftwiderstand | ||
| + | ::-Keine Exakte Pendellänge | ||
| + | ::-Reaktion an der Stopuhr | ||
| + | ::-Reibung am Schwingungsurprung (?!) | ||
| + | |||
| + | :Die Abweichungen ergeben sich wegen den Messfehlern für die Pendellänge und der Schwingungsdauer. | ||
| + | |||
| + | Grafische Darstellung: | ||
| + | |||
| + | |||
| + | <ggb_applet height="400" width="700" filename="Messwerte_Markus.ggb" /> | ||
| + | |||
| + | |||
| + | |||
---- | ---- | ||
Version vom 22. Januar 2010, 11:59 Uhr
Thomas, Sebastian, Elena, Tina
| Auslenkung | Pendellänge | Durchschnittliche Schwingungsdauer | Durchschnittliche Beschleunigung | Abweichung von g=9,81 m/s² in % |
| 20° | 5 cm | 0,58 s | 5,9 m/s² | 40 |
| 20° | 10 cm | 0,73 s | 7,4 m/s² | 25 |
| 20° | 20 cm | 0,95 s | 8,7 m/s² | 11 |
| 20° | 30 cm | 1,15 s | 9,0 m/s² | 8 |
| 20° | 40 cm | 1,33 s | 8,9 m/s² | 9 |
Durch die Reaktionszeit kommt es zu leichten bis staken Abweichungen der Beschleunigung vn g. Bei der Durchführung unserer Messungen haben wir jeweils 10 Schwingungen gemessen, damit unsere Werte genauer sind.
| Auslenkung | Pendellänge | Durchschnittliche Schwingungsdauer |
| 20° | 70 cm | 1,7 s |
| 20° | 37 cm | 1,25 s |
| 20° | 17 cm | 0,9 s |
| 20° | 75 cm | 1,75 s |
| 45° | 75 cm | 1,75 s |
Albin, Patrik, Christoph, Dominik:
| Auslenkung | Pendellänge | Durchschnittliche Schwingungsdauer |
| 20° | 70 cm | 1,7 s |
| 20° | 37 cm | 1,25 s |
| 20° | 17 cm | 0,9 s |
| 20° | 75 cm | 1,75 s |
| 45° | 75 cm | 1,75 s |
Werte mit anderem Gewicht: Keine Änderung.
Folgerung: Die Schwingungsdauer hängt nur mit der Länge des Pendels zusammen, nicht mit der Masse des angehängten Gewichts und der Auslenkung.
Julian Rudolph, Felix Göller, Markus Fischer:
Benötigte Materialien:
- -Metermaß
- -Schnur
- -Gewichtsstück(e)
- -Stopuhr
- -Haken zum Befestigen
Durchführung:
Zuerst hängt man die Schnur mit dem Gewichtsstück an den Haken vom Stab. Dann misst man erst 10cm Schnurlänge. Nun lenkt man das Gewichtsstück mit der Schnur um etwa 20° vom Stab weg aus der senkrechten, und lassen es dann los. Ab diesem Moment messen wir 10 Schwingungen.
Dann macht man das gleiche mit 20cm, 30cm, 40cm, 50cm.
Die Auslenkung muss nicht genau 20° sein, sie kann auch nur 10° sein, das Ergebnis (Schwingungsdauer ist die selbe). Auch wieviel Gewicht an der Schnur hängt spielt keine Rolle. Vielleicht würde mehr Gewicht die Reibung erhöhen und dadurch die Messwerte nochmehr verfälschen...
| Pendellänge l in cm | Schwingungsdauer T in s |
| 10 | 6,3 |
| 20 | 9,0 |
| 30 | 11,0 |
| 40 | 12,6 |
| 50 | 14,2 |
Daraus ergibt sich pro Schwingung eine Zeit von:
- Für 10 cm: 0,63s
- Für 20 cm: 0,90s
- Für 30 cm: 1,10s
- Für 40 cm: 1,26s
- Für 50 cm: 1,42s
Anmerkungen:
Für 10 cm: Fallbeschleunigung g = 9,95 m/s2
Für 20 cm: Fallbeschleunigung g = 9,74 m/s2
Für 30 cm: Fallbeschleunigung g = 9,79 m/s2
Für 40 cm: Fallbeschleunigung g = 9,95 m/s2
Für 50 cm: Fallbeschleunigung g = 9,79 m/s2
Abweichungen durch folgende Gründe:
- -Luftwiderstand
- -Keine Exakte Pendellänge
- -Reaktion an der Stopuhr
- -Reibung am Schwingungsurprung (?!)
- Die Abweichungen ergeben sich wegen den Messfehlern für die Pendellänge und der Schwingungsdauer.
Grafische Darstellung:
Babara, Lea, Felix K., Simon
50g
| Pendellänge l in cm | Schwingungsdauer T in s |
| 52 | 14,5 |
| 37 | 12 |
| 62 | 17 |
| 16 | 7,7 |
150g
| Pendellänge l in cm | Schwingungsdauer T in s |
| 35 | 12,2 |
| 40 | 13,1 |
Die Schwingungsdauer ist auch mit mehreren Gewichtsstücken gleich
Katharina, Christian, Anna-Theresa, Nicole und Julia
| Auslenkung | Pendellänge | Durchschnittliche Schwingungsdauer | Fallbeschleunigung g (Abweichung) |
| 20° | 18,5 cm | 0,88 s | 9,43 m/s² (3,9%) |
| 20° | 26,0 cm | 1,07 s | 8,97 m/s² (8,6%) |
| 20° | 35,0 cm | 1,22 s | 9,28 m/s² (5,4%) |
| 20° | 47,0 cm | 1,36 s | 9,94 m/s² (1,3%) |
Durch die Messfehler bei der Pendellänge und der Schwingungsdauer ergeben sich Ungenauigkeiten.