Benutzer:Luisa Metzner: Unterschied zwischen den Versionen
| Zeile 13: | Zeile 13: | ||
*[[Benutzer:Miriam Abert|Miriam]] | *[[Benutzer:Miriam Abert|Miriam]] | ||
*[[Benutzer:Melissa Eller|Melissa]] | *[[Benutzer:Melissa Eller|Melissa]] | ||
| − | + | ||
==Meine Projektbeiträge== | ==Meine Projektbeiträge== | ||
'''Wie viele Quadrate gibt es auf einem Schachbrett? ''' | '''Wie viele Quadrate gibt es auf einem Schachbrett? ''' | ||
| Zeile 70: | Zeile 70: | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
<strong> <math>\frac{36}{400}</math> </strong> < <strong> <math>12%</math> </strong> < <strong> <math>0,78 </math> </strong> < <strong> <math>\frac{40}{50}</math> </strong> | <strong> <math>\frac{36}{400}</math> </strong> < <strong> <math>12%</math> </strong> < <strong> <math>0,78 </math> </strong> < <strong> <math>\frac{40}{50}</math> </strong> | ||
| + | </div> | ||
| + | |||
| + | |||
| + | ==Erweitern und Kürzen== | ||
| + | <div class="lueckentext-quiz"> | ||
| + | |||
| + | Beim <strong> Erweitern </strong> und <strong> Kürzen </strong> muss man Zähler und <strong> Nenner </strong> mit der gleichen Zahl multiplizieren bzw. dividieren. | ||
| + | Beim Umwandeln in einen <strong> Dezimalbruch </strong> bzw. in <strong> Prozent </strong> muss man den Nenner erst auf eine Stufenzahl bringen. | ||
| + | |||
| + | Ausnahme: Wenn man den Nenner nicht auf eine <strong> Stufenzahl </strong> bringen kann, dividiert man <strong> Zähler </strong> durch Nenner um einen Dezimalbruch zu erhalten. | ||
| + | |||
</div> | </div> | ||
Version vom 16. Februar 2009, 08:12 Uhr
Hallo erst mal!Mein Name ist Luisa.Ich gehe aufs Gymnasium und bin in der 5a (Regiomontanus Gymnasium Haßfurt).2008 ist das Jahr der Mathematik.Für unsere Klasse gibt es auch eine Seite (Klasse 5a).
Dies sind alle meine Freundinnen auf dem Gymnasium:
Meine Projektbeiträge
Wie viele Quadrate gibt es auf einem Schachbrett?
Nein, keine 64, auch keine 65 Quadrate.
Hier eine kleine Hilfe:
64+?
Lösungsidee
1. Schritt:
3x3 Quadrat 3x3 Quadrat 3x3 Quadrat 9 kleine 4 sich überlappende 1 großes Quadrate Quadrate Quadrat
2. Schritt:
4x4 Quadrat 4x4 Quadrat 4x4 Quadrat 4x4 Quadrat 16 kleine 9 sich überlappende 4 sich überlappende 1 großes Quadrate Quadarate Quadrate Quadrat
Lösung durch Makieren des blauen Feldes sichtbar machen:
8²+7²+6²+5²+4²+3²+2²+1²=204
Ordne die Brüche nach der Größe
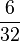 <
< 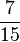 <
<  <
< 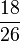
 <
<  <
< 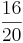 <
< 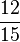
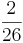 <
< 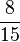 <
<  <
< 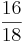
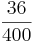 <
< 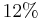 <
< 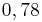 <
< 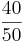
Erweitern und Kürzen
Beim Erweitern und Kürzen muss man Zähler und Nenner mit der gleichen Zahl multiplizieren bzw. dividieren. Beim Umwandeln in einen Dezimalbruch bzw. in Prozent muss man den Nenner erst auf eine Stufenzahl bringen.
Ausnahme: Wenn man den Nenner nicht auf eine Stufenzahl bringen kann, dividiert man Zähler durch Nenner um einen Dezimalbruch zu erhalten.