1. Dezember: Unterschied zwischen den Versionen
Aus RMG-Wiki
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 10: | Zeile 10: | ||
:Ich hab die selbe Lsg wie Frau Eirich, da du unten aus der Lage der Pkt D un G die Steigung des Graphn ausrechenen kannst... Lässt du nun die Parallele durch D laufn, dann is der Abstand diese genannten 5,37 ! Du kannst natürlich auch die Steigung von D und G ausrechnen und die Parallele dazu einzeichnen, da erhälst du wie du richtig geschrieben hast 4,75... Die Frage war ja...Wie breit ist die Strecke auf Zentimeter gerundet, die die Federwichtel '''idealerweise''' durch das Dorf führen? Also würd ich die von Frau Maria Eirich genannten 5,37 vorschlagen, da die Strecke ja breiter is und die wollen ja überholen mfg [[Benutzer:Neutert Jan-Peter|Neutert Jan-Peter]] <small>19:39, 1. Dez. 2008 (UTC)</small> | :Ich hab die selbe Lsg wie Frau Eirich, da du unten aus der Lage der Pkt D un G die Steigung des Graphn ausrechenen kannst... Lässt du nun die Parallele durch D laufn, dann is der Abstand diese genannten 5,37 ! Du kannst natürlich auch die Steigung von D und G ausrechnen und die Parallele dazu einzeichnen, da erhälst du wie du richtig geschrieben hast 4,75... Die Frage war ja...Wie breit ist die Strecke auf Zentimeter gerundet, die die Federwichtel '''idealerweise''' durch das Dorf führen? Also würd ich die von Frau Maria Eirich genannten 5,37 vorschlagen, da die Strecke ja breiter is und die wollen ja überholen mfg [[Benutzer:Neutert Jan-Peter|Neutert Jan-Peter]] <small>19:39, 1. Dez. 2008 (UTC)</small> | ||
| − | Ich hab auch mal eine Skizze erstellt und versucht, die Strecke einzuzeichnen. Dabei bin ich auf eine Breite von ca. 5,40m gekommen, daher würd ich auch sagen, dass 5,37m die richtige Lösung ist. | + | Ich hab auch mal eine Skizze erstellt und versucht, die Strecke einzuzeichnen. Dabei bin ich auf eine Breite von ca. 5,40m gekommen, daher würd ich auch sagen, dass 5,37m die richtige Lösung ist. Gruß -- [[Benutzer:Wilk Florian|Wilk Florian]] <small>21:47, 1. Dez. 2008 (UTC)</small> |
| + | |||
| − | |||
nach 100 maligem umstellen und hin und her bin ich auf 5,47 gekommen. und wenn man dann die lösung sucht, die am nähestem dran is, dann komme ich auch auf die 5,37 ;) | nach 100 maligem umstellen und hin und her bin ich auf 5,47 gekommen. und wenn man dann die lösung sucht, die am nähestem dran is, dann komme ich auch auf die 5,37 ;) | ||
| Zeile 18: | Zeile 18: | ||
[[Bild:adventsbild.png]] | [[Bild:adventsbild.png]] | ||
| − | + | das is meine Lösung ;), ich komm auch auf 5, 37 | |
| − | + | -- [[Benutzer:Baumüller Lukas|Lukas Baumüller]] <small>21:50, 1. Dez. 2008 (UTC)</small> | |
Aktuelle Version vom 1. Dezember 2008, 22:50 Uhr
Hm also ich hab mal so n PLan in Excel aufgestellt. Kp ob des so geht^^
Die Lösung wär dann 4,75m.-- Kundmüller Maximilian 17:40, 1. Dez. 2008 (UTC)
- Die Lösung 4,75 ergibt sich wenn man die Gerade durch DG legt. Allerdings ist der Abstand D von der Geraden durch J und M 5,37 (siehe Datei:Kerze1 08.ggb) ..wäre also breiter....-- Maria Eirich 17:54, 1. Dez. 2008 (UTC)
- Ich hab die selbe Lsg wie Frau Eirich, da du unten aus der Lage der Pkt D un G die Steigung des Graphn ausrechenen kannst... Lässt du nun die Parallele durch D laufn, dann is der Abstand diese genannten 5,37 ! Du kannst natürlich auch die Steigung von D und G ausrechnen und die Parallele dazu einzeichnen, da erhälst du wie du richtig geschrieben hast 4,75... Die Frage war ja...Wie breit ist die Strecke auf Zentimeter gerundet, die die Federwichtel idealerweise durch das Dorf führen? Also würd ich die von Frau Maria Eirich genannten 5,37 vorschlagen, da die Strecke ja breiter is und die wollen ja überholen mfg Neutert Jan-Peter 19:39, 1. Dez. 2008 (UTC)
Ich hab auch mal eine Skizze erstellt und versucht, die Strecke einzuzeichnen. Dabei bin ich auf eine Breite von ca. 5,40m gekommen, daher würd ich auch sagen, dass 5,37m die richtige Lösung ist. Gruß -- Wilk Florian 21:47, 1. Dez. 2008 (UTC)
nach 100 maligem umstellen und hin und her bin ich auf 5,47 gekommen. und wenn man dann die lösung sucht, die am nähestem dran is, dann komme ich auch auf die 5,37 ;) (ich hoffe mal die andern aufgabend sind auch so "schwer")
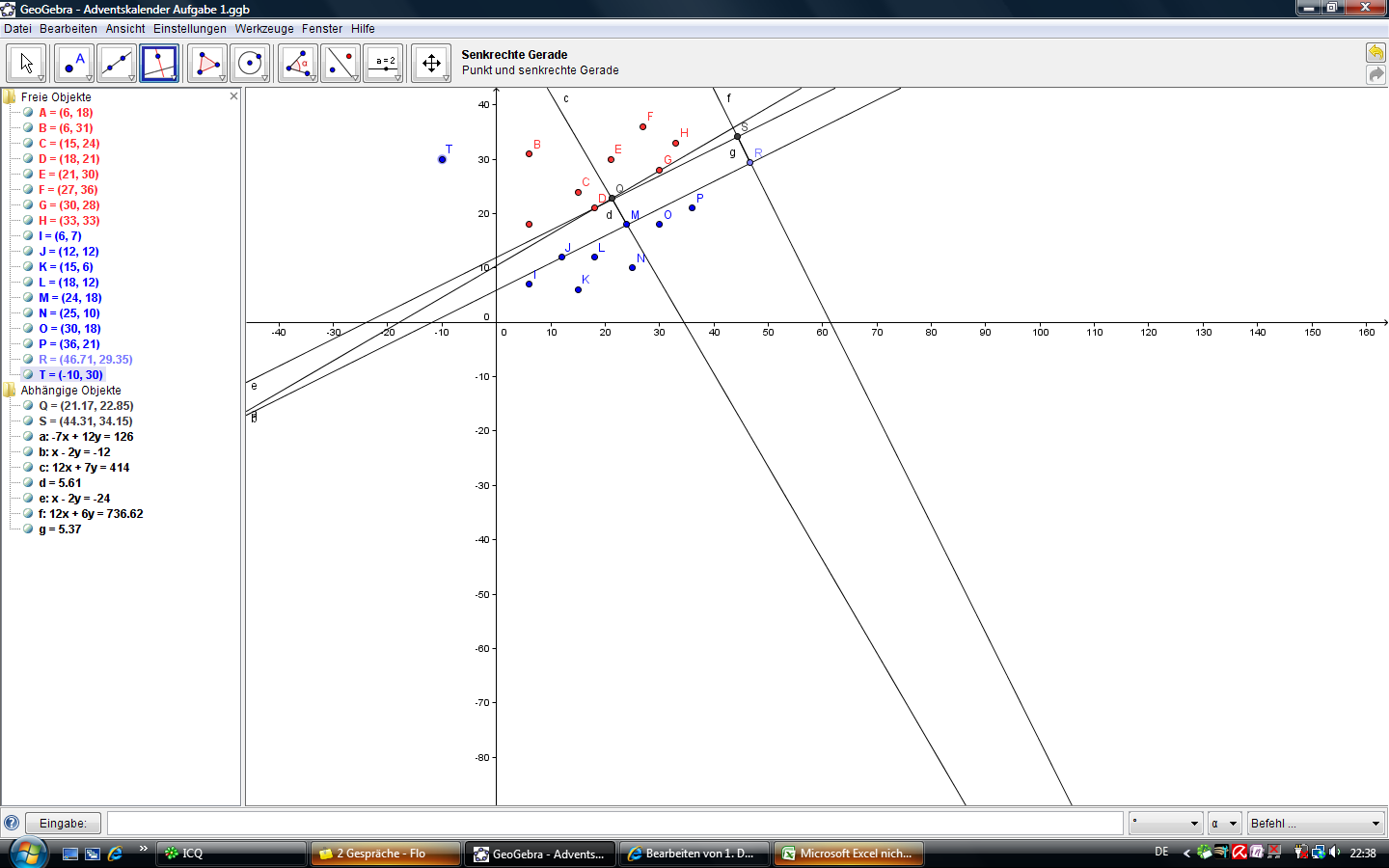 das is meine Lösung ;), ich komm auch auf 5, 37
-- Lukas Baumüller 21:50, 1. Dez. 2008 (UTC)
das is meine Lösung ;), ich komm auch auf 5, 37
-- Lukas Baumüller 21:50, 1. Dez. 2008 (UTC)

